III Abstraction

Many of our data definitions and function definitions look alike. For example, the definition for a list of Strings differs from that of a list of Numbers in only two places: the names of the classes of data and the words “String” and “Number.” Similarly, a function that looks for a specific string in a list of Strings is nearly indistinguishable from one that looks for a specific number in a list of Numbers.

Experience shows that these kinds of similarities are problematic. The similarities come about because programmers—physically or mentally—copy code. When programmers are confronted with a problem that is roughly like another one, they copy the solution and modify the new copy to solve the new problem. You will find this behavior both in “real” programming contexts as well as in the world of spreadsheets and mathematical modeling. Copying code, however, means that programmers copy mistakes, and the same fix may have to be applied to many copies. It also means that when the underlying data definition is revised or extended, all copies of code must be found and modified in a corresponding way. This process is both expensive and error-prone, imposing unnecessary costs on programming teams.

Good programmers try to eliminate similarities as much as the programming language allows.A program is like an essay. The first version is a draft, and drafts demand editing. “Eliminate” implies that programmers write down their first drafts of programs, spot similarities (and other problems), and get rid of them. For the last step, they either abstract or use existing (abstract) functions. It often takes several iterations of this process to get the program into satisfactory shape.

The first half of this part shows how to abstract over similarities in functions and data definitions. Programmers also refer to the result of this process as an abstraction, conflating the name of the process and its result. The second half is about the use of existing abstractions and new language elements to facilitate this process. While the examples in this part are taken from the realm of lists, the ideas are universally applicable.

14 Similarities Everywhere🔗

If you solved (some of) the exercises in Arbitrarily Large Data, you know that many solutions look alike. As a matter of fact, the similarities may tempt you to copy the solution of one problem to create the solution for the next. But thou shall not steal code, not even your own. Instead, you must abstract over similar pieces of code and this chapter teaches you how to abstract.

Our means of avoiding similarities are specific to “Intermediate Student Language” or ISL for short.In DrRacket, choose “Intermediate Student” from the “How to Design Programs” submenu in the “Language” menu. Almost all other programming languages provide similar means; in object-oriented languages you may find additional abstraction mechanisms. Regardless, these mechanisms share the basic characteristics spelled out in this chapter, and thus the design ideas explained here apply in other contexts, too.

14.1 Similarities in Functions🔗

The design recipe determines a function’s basic organization because the template is created from the data definition without regard to the purpose of the function. Not surprisingly, then, functions that consume the same kind of data look alike.

; Los -> Boolean
; does l contain "dog"
(define (contains-dog? l)
  (cond
    [(empty? l) #false]
    [else
     (or
       (string=? (first l)
                 "dog")
       (contains-dog?
         (rest l)))]))

; Los -> Boolean
; does l contain "cat"
(define (contains-cat? l)
  (cond
    [(empty? l) #false]
    [else
     (or
       (string=? (first l)
                 "cat")
       (contains-cat?
         (rest l)))]))
Figure 86: Two similar functions

Consider the two functions in figure 86, which consume lists of strings and look for specific strings. The function on the left looks for "dog", the one on the right for "cat". The two functions are nearly indistinguishable. Each consumes lists of strings; each function body consists of a cond expression with two clauses. Each produces #false if the input is '(); each uses an or expression to determine whether the first item is the desired item and, if not, uses recursion to look in the rest of the list. The only difference is the string that is used in the comparison of the nested cond expressions: contains-dog? uses "dog" and contains-cat? uses "cat". To highlight the differences, the two strings are shaded.

Good programmers are too lazy to define several closely related functions. Instead they define a single function that can look for both a "dog" and a "cat" in a list of strings. This general function consumes an additional piece of data—the string to look for—and is otherwise just like the two original functions:

; String Los -> Boolean
; determines whether l contains the string s
(define (contains? s l)
  (cond
    [(empty? l) #false]
    [else (or (string=? (first l) s)
              (contains? s (rest l)))]))

If you really needed a function such as contains-dog? now, you could define it as a one-line function, and the same is true for the contains-cat? function. Figure 87 does just that, and you should briefly compare it with figure 86 to make sure you understand how we get from there to here. Best of all, though, with contains? it is now trivial to look for any string in a list of strings and there is no need to ever define a specialized function such as contains-dog? again.

; Los -> Boolean
; does l contain "dog"
(define (contains-dog? l)
  (contains? "dog" l))

; Los -> Boolean
; does l contain "cat"
(define (contains-cat? l)
  (contains? "cat" l))
Figure 87: Two similar functions, revisited

What you haveComputer scientists borrow the term “abstract” from mathematics. There, “6” is an abstract concept because it represents all ways of enumerating six things. In contrast, “6 inches” or “6 eggs” are concrete uses. just witnessed is called abstraction or, more precisely, functional abstraction. Abstracting different versions of functions is one way to eliminate similarities from programs, and as you will see, removing similarities simplifies keeping a program intact over a long period.

Exercise 235. Use the contains? function to define functions that search for "atom", "basic", and "zoo", respectively.

Exercise 236. Create test suites for the following two functions:

; Lon -> Lon
; adds 1 to each item on l
(define (add1* l)
  (cond
    [(empty? l) '()]
    [else
     (cons
       (add1 (first l))
       (add1* (rest l)))]))

; Lon -> Lon
; adds 5 to each item on l
(define (plus5 l)
  (cond
    [(empty? l) '()]
    [else
     (cons
       (+ (first l) 5)
       (plus5 (rest l)))]))

Then abstract over them. Define the above two functions in terms of the abstraction as one-liners and use the existing test suites to confirm that the revised definitions work properly. Finally, design a function that subtracts 2 from each number on a given list.

14.2 Different Similarities🔗

Abstraction looks easy in the case of the contains-dog? and contains-cat? functions. It takes only a comparison of two function definitions, a replacement of a literal string with a function parameter, and a quick check that it is easy to define the old functions with the abstract function. This kind of abstraction is so natural that it showed up in the preceding two parts of the book without much ado.

This section illustrates how the very same principle yields a powerful form of abstraction. Take a look at figure 88. Both functions consume a list of numbers and a threshold. The left one produces a list of all those numbers that are below the threshold, while the one on the right produces all those that are above the threshold.

; Lon Number -> Lon
; select those numbers on l
; that are below t
(define (small l t)
  (cond
    [(empty? l) '()]
    [else
     (cond
       [(< (first l) t)
        (cons (first l)
          (small
            (rest l) t))]
       [else
        (small
          (rest l) t)])]))

; Lon Number -> Lon
; select those numbers on l
; that are above t
(define (large l t)
  (cond
    [(empty? l) '()]
    [else
     (cond
       [(> (first l) t)
        (cons (first l)
          (large
            (rest l) t))]
       [else
        (large
          (rest l) t)])]))
Figure 88: Two more similar functions

The two functions differ in only one place: the comparison operator that determines whether a number from the given list should be a part of the result or not. The function on the left uses <, and the right one >. Other than that, the two functions look identical, not counting the function name.

Let’s follow the first example and abstract over the two functions with an additional parameter. This time the additional parameter represents a comparison operator rather than a string:

(define (extract R l t)
  (cond
    [(empty? l) '()]
    [else (cond
            [(R (first l) t)
             (cons (first l)
                   (extract R (rest l) t))]
            [else
             (extract R (rest l) t)])]))

To apply this new function, we must supply three arguments: a function R that compares two numbers, a list l of numbers, and a threshold t. The function then extracts all those items i from l for which (R i t) evaluates to #true.

Stop! At this point you should ask whether this definition makes any sense. Without further fuss, we have created a function that consumes a function—something that you probably have not seen before.If you have taken a calculus course, you have encountered the differential operator and the indefinite integral. Both of those are functions that consume and produce functions. But we do not assume that you have taken a calculus course. It turns out, however, that your simple little teaching language ISL supports these kinds of functions, and that defining such functions is one of the most powerful tools of good programmers—even in languages in which function-consuming functions do not seem to be available.

Testing shows that (extract < l t) computes the same result as (small l t):

(check-expect (extract < '() 5) (small '() 5))
(check-expect (extract < '(3) 5) (small '(3) 5))
(check-expect (extract < '(1 6 4) 5)
(small '(1 6 4) 5))

Similarly, (extract > l t) produces the same result as (large l t), which means that you can define the two original functions like this:

; Lon Number -> Lon
(define (small-1 l t)
  (extract < l t))

; Lon Number -> Lon
(define (large-1 l t)
  (extract > l t))

The important insight is not that small-1 and large-1 are one-line definitions. Once you have an abstract function such as extract, you can put it to good uses elsewhere:

(extract = l t): This expression extracts all those numbers in l that are equal to t.
(extract <= l t): This one produces the list of numbers in l that are less than or equal to t.
(extract >= l t): This last expression computes the list of numbers that are greater than or equal to the threshold.

As a matter of fact, the first argument for extract need not be one of ISL’s pre-defined operations. Instead, you can use any function that consumes two arguments and produces a Boolean. Consider this example:

; Number Number -> Boolean
; is the area of a square with side x larger than c
(define (squared>? x c)
(> (* x x) c))

That is, squared>? checks whether the claim x2 > c holds, and it is usable with extract:

(extract squared>? (list 3 4 5) 10)

This application extracts those numbers in (list 3 4 5) whose square is larger than 10.

Exercise 237. Evaluate (squared>? 3 10) and (squared>? 4 10) in DrRacket. How about (squared>? 5 10)?

So far you have seen that abstracted function definitions can be more useful than the original functions. For example, contains? is more useful than contains-dog? and contains-cat?, and extract is more useful than small and large.These benefits of abstraction are available at all levels of programming: word documents, spreadsheets, small apps, and large industrial projects. Creating abstractions for the latter drives research on programming languages and software engineering. Another important aspect of abstraction is that you now have a single point of control over all these functions. If it turns out that the abstract function contains a mistake, fixing its definition suffices to fix all other definitions. Similarly, if you figure out how to accelerate the computations of the abstract function or how to reduce its energy consumption, then all functions defined in terms of this function are improved without any extra effort. The following exercises indicate how these single-point-of-control improvements work.

; Nelon -> Number
; determines the smallest
; number on l
(define (inf l)
  (cond
    [(empty? (rest l))
     (first l)]
    [else
     (if (< (first l)
            (inf (rest l)))
         (first l)
         (inf (rest l)))]))

; Nelon -> Number
; determines the largest
; number on l
(define (sup l)
  (cond
    [(empty? (rest l))
     (first l)]
    [else
     (if (> (first l)
            (sup (rest l)))
         (first l)
         (sup (rest l)))]))
Figure 89: Finding the inf and sup in a list of numbers

Exercise 238. Abstract the two functions in figure 89 into a single function. Both consume non-empty lists of numbers (Nelon) and produce a single number. The left one produces the smallest number in the list, and the right one the largest.

Define inf-1 and sup-1 in terms of the abstract function. Test them with these two lists:

(list 25 24 23 22 21 20 19 18 17 16 15 14 13
12 11 10 9 8 7 6 5 4 3 2 1)

(list 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25)

Why are these functions slow on some of the long lists?

Modify the original functions with the use of max, which picks the larger of two numbers, and min, which picks the smaller one. Then abstract again, define inf-2 and sup-2, and test them with the same inputs again. Why are these versions so much faster?

For another answer to these questions, see Local Definitions.

14.3 Similarities in Data Definitions🔗

Now take a close look at the following two data definitions:

; An Lon (List-of-numbers)
; is one of:
; – '()
; – (cons Number Lon)

; An Los (List-of-String)
; is one of:
; – '()
; – (cons String Los)

The one on the left introduces lists of numbers; the one on the right describes lists of strings. And the two data definitions are similar. Like similar functions, the two data definitions use two different names, but this is irrelevant because any name would do. The only real difference concerns the first position inside of cons in the second clause, which specifies what kind of items the list contains.

In order to abstract over this one difference, we proceed as if a data definition were a function. We introduce a parameter, which makes the data definition look like a function, and where there used to be different references, we use this parameter:

; A [List-of ITEM] is one of:
; – '()
; – (cons ITEM [List-of ITEM])

We call such abstract data definitions parametric data definitions because of the parameter. Roughly speaking, a parametric data definition abstracts from a reference to a particular collection of data in the same manner as a function abstracts from a particular value.

The question is, of course, what these parameters range over. For a function, they stand for an unknown value; when the function is applied, the value becomes known. For a parametric data definition, a parameter stands for an entire class of values. The process of supplying the name of a data collection to a parametric data definition is called instantiation; here are some sample instantiations of the List-of abstraction:

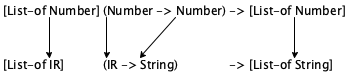
When we write [List-of Number], we are saying that ITEM represents all numbers so it is just another name for List-of-numbers;
Similarly, [List-of String] defines the same class of data as List-of-String; and
If we had identified a class of inventory records, like this:
(define-struct IR [name price])
; An IR is a structure:
; (make-IR String Number)
then [List-of IR] would be a name for the lists of inventory records.

By convention, we use names with all capital letters for parameters of data definitions, while the arguments are spelled as needed.

Our way to validate that these short-hands really mean what we say they mean is to substitute the actual name of a data definition, for example, Number, for the parameter ITEM of the data definition and to use a plain name for the data definition:

; A List-of-numbers-again is one of:
; – '()
; – (cons Number List-of-numbers-again)

Since the data definition is self-referential, we copied the entire data definition. The resulting definition looks exactly like the conventional one for lists of numbers and truly identifies the same class of data.

Let’s take a brief look at a second example, starting with a structure type definition:

(define-struct point [hori veri])

Here are two different data definitions that use this structure type:

; A Pair-boolean-string is a structure:
; (make-point Boolean String)

; A Pair-number-image is a structure:
; (make-point Number Image)

In this case, the data definitions differ in two places—both marked by highlighting. The differences in the hori fields correspond to each other, and so do the differences in the veri fields. It is thus necessary to introduce two parameters to create an abstract data definition:

; A [CP H V] is a structure:
; (make-point H V)

Here H is the parameter for data collections for the hori field, and V stands for data collections that can show up in the veri field.

To instantiate a data definition with two parameters, you need two names of data collections. Using Number and Image for the parameters of CP, you get [CP Number Image], which describes the collections of points that combine a number with an image. In contrast [CP Boolean String] combines Boolean values with strings in a point structure.

Exercise 239. A list of two items is another frequently used form of data in ISL programming. Here is a data definition with two parameters:

; A [List X Y] is a list:
; (cons X (cons Y '()))

Instantiate this definition to describe the following classes of data:

pairs of Numbers,
pairs of Numbers and 1Strings, and
pairs of Strings and Booleans.

Also make one concrete example for each of these three data definitions.

Once you have parametric data definitions, you can mix and match them to great effect. Consider this one:

; [List-of [CP Boolean Image]]

The outermost notation is [List-of ...], which means that you are dealing with a list. The question is what kind of data the list contains, and to answer that question, you need to study the inside of the List-of expression:

; [CP Boolean Image]

This inner part combines Boolean and Image in a point. By implication,

; [List-of [CP Boolean Image]]

is a list of points that combine Booleans and Images. Similarly,

; [CP Number [List-of Image]]

is an instantiation of CP that combines one Number with a list of Images.

Exercise 240. Here are two strange but similar data definitions:

; An LStr is one of:
; – String
; – (make-layer LStr)

; An LNum is one of:
; – Number
; – (make-layer LNum)

Both data definitions rely on this structure-type definition:

(define-struct layer [stuff])

Both define nested forms of data: one is about numbers and the other about strings. Make examples for both. Abstract over the two. Then instantiate the abstract definition to get back the originals.

Exercise 241. Compare the definitions for NEList-of-temperatures and NEList-of-Booleans. Then formulate an abstract data definition NEList-of.

Exercise 242. Here is one more parametric data definition:

; A [Maybe X] is one of:
; – #false
; – X

Interpret these data definitions: [Maybe String], [Maybe [List-of String]], and [List-of [Maybe String]].

What does the following function signature mean:

; String [List-of String] -> [Maybe [List-of String]]
; returns the remainder of los starting with s
; #false otherwise
(check-expect (occurs "a" (list "b" "a" "d" "e"))
(list "d" "e"))
(check-expect (occurs "a" (list "b" "c" "d")) #false)
(define (occurs s los)
los)

Work through the remaining steps of the design recipe.

14.4 Functions Are Values🔗

The functions in this part stretch our understanding of program evaluation. It is easy to understand how functions consume more than numbers, say strings or images. Structures and lists are a bit of a stretch, but they are finite “things” in the end. Function-consuming functions, however, are strange. Indeed, the very idea violates the first intermezzo in two ways: (1) the names of primitives and functions are used as arguments in applications, and (2) parameters are used in the function position of applications.

Spelling out the problem tells you how the ISL grammar differs from BSL’s. First, our expression language should include the names of functions and primitive operations in the definition. Second, the first position in an application should allow things other than function names and primitive operations; at a minimum, it must allow variables and function parameters.

The changes to the grammar seem to demand changes to the evaluation rules, but all that changes is the set of values. Specifically, to accommodate functions as arguments of functions, the simplest change is to say that functions and primitive operations are values.

Exercise 243. Assume the definitions area in DrRacket contains

(define (f x) x)

Identify the values among the following expressions:

(cons f '())
(f f)
(cons f (cons 10 (cons (f 10) '())))

Explain why they are (not) values.

Exercise 244. Argue why the following sentences are now legal:

(define (f x) (x 10))
(define (f x) (x f))
(define (f x y) (x 'a y 'b))

Explain your reasoning.

Exercise 245. Develop the function=at-1.2-3-and-5.775? function. Given two functions from numbers to numbers, the function determines whether the two produce the same results for 1.2, 3, and -5.775.

Mathematicians say that two functions are equal if they compute the same result when given the same input—for all possible inputs.

Can we hope to define function=?, which determines whether two functions from numbers to numbers are equal? If so, define the function. If not, explain why and consider the implication that you have encountered the first easily definable idea for which you cannot define a function.

14.5 Computing with Functions🔗

The switch from BSL+ to ISL allows the use of functions as arguments and the use of names in the first position of an application. DrRacket deals with names in these positions like anywhere else, but naturally, it expects a function as a result. Surprisingly, a simple adaptation of the laws of algebra suffices to evaluate programs in ISL.

Let’s see how this works for extract from Different Similarities. Obviously,

(extract < '() 5) == '()

holds. We can use the law of substitution from Intermezzo 1: Beginning Student Language and continue computing with the body of the function. Like so many times, the parameters, R, l, and t, are replaced by their arguments, <, '(), and 5, respectively. From here, it is plain arithmetic, starting with the conditionals:

==
(cond
[(empty? '()) '()]
[else (cond
        [(< (first '()) t)
         (cons (first '()) (extract < (rest '()) 5))]
        [else (extract < (rest '()) 5)])])
==
(cond
[#true '()]
[else (cond
        [(< (first '()) t)
         (cons (first '()) (extract < (rest '()) 5))]
        [else (extract < (rest '()) 5)])])
== '()

Next we look at a one-item list:

(extract < (cons 4 '()) 5)

The result should be (cons 4 '()) because the only item of this list is 4 and (< 4 5) is true. Here is the first step of the evaluation:

(extract < (cons 4 '()) 5)
==
(cond
  [(empty? (cons 4 '())) '()]
  [else (cond
          [(< (first (cons 4 '())) 5)
           (cons (first (cons 4 '()))
                 (extract < (rest (cons 4 '())) 5))]
          [else (extract < (rest (cons 4 '())) 5)])])

Again, all occurrences of R are replaced by <, l by (cons 4 '()), and t by 5. The rest is straightforward:

(cond
  [(empty? (cons 4 '())) '()]
  [else (cond
          [(< (first (cons 4 '())) 5)
           (cons (first (cons 4 '()))
                 (extract < (rest (cons 4 '())) 5))]
          [else (extract < (rest (cons 4 '())) 5)])])
==
(cond
  [#false '()]
  [else (cond
          [(< (first (cons 4 '())) 5)
           (cons (first (cons 4 '()))
                 (extract < (rest (cons 4 '())) 5))]
          [else (extract < (rest (cons 4 '())) 5)])])
==
(cond
  [(< (first (cons 4 '())) 5)
   (cons (first (cons 4 '()))
         (extract < (rest (cons 4 '())) 5))]
  [else (extract < (rest (cons 4 '())) 5)])

==
(cond
  [(< 4 5)
   (cons (first (cons 4 '()))
         (extract < (rest (cons 4 '())) 5))]
  [else (extract < (rest (cons 4 '())) 5)])

This is the key step, with < used after being substituted into this position. And it continues with arithmetic:

==
(cond
  [#true
   (cons (first (cons 4 '()))
         (extract < (rest (cons 4 '())) 5))]
  [else (extract < (rest (cons 4 '())) 5)])
==
(cons 4 (extract < (rest (cons 4 '())) 5))
==
(cons 4 (extract < '() 5))
==
(cons 4 '())

The last step is the equation from above, meaning we can apply the law of substituting equals for equals.

Our final example is an application of extract to a list of two items:

(extract < (cons 6 (cons 4 '())) 5)
== (extract < (cons 4 '()) 5)
== (cons 4 (extract < '() 5))
== (cons 4 '())

Step 1 is new. It deals with the case that extract eliminates the first item on the list if it is not below the threshold.

Exercise 246. Check step 1 of the last calculation

(extract < (cons 6 (cons 4 '())) 5)
==
(extract < (cons 4 '()) 5)

using DrRacket’s stepper.

Exercise 247. Evaluate (extract < (cons 8 (cons 4 '())) 5) with DrRacket’s stepper.

Exercise 248. Evaluate (squared>? 3 10) and (squared>? 4 10) in DrRacket’s stepper.

Consider this interaction:

> (extract squared>? (list 3 4 5) 10)
(list 4 5)

Here are some steps as the stepper would show them:

(extract squared>? (list 3 4 5) 10)

(1)
==
(cond
  [(empty? (list 3 4 5)) '()]
  [else
    (cond
      [(squared>? (first (list 3 4 5)) 10)
       (cons (first (list 3 4 5))
             (extract squared>?
                      (rest (list 3 4 5))
                      10))]
      [else (extract squared>?
                     (rest (list 3 4 5))
                     10)])])

(2)
== ... ==
(cond
  [(squared>? 3 10)
   (cons (first (list 3 4 5))
         (extract squared>?
                  (rest (list 3 4 5))
                  10))]
  [else (extract squared>?
                 (rest (list 3 4 5))
                 10)])

(3)

Use the stepper to confirm the step from lines (1) to (2). Continue the stepping to fill in the gaps between steps (2) and (3). Explain each step as the use of a law.

Exercise 249. Functions are values: arguments, results, items in lists. Place the following definitions and expressions into DrRacket’s definitions window and use the stepper to find out how running this program works:

(define (f x) x)
(cons f '())
(f f)
(cons f (cons 10 (cons (f 10) '())))

The stepper displays functions as lambda expressions; see Nameless Functions.

15 Designing Abstractions🔗

In essence, to abstract is to turn something concrete into a parameter. We have this several times in the preceding section. To abstract similar function definitions, you add parameters that replace concrete values in the definition. To abstract similar data definitions, you create parametric data definitions. When you encounter other programming languages, you will see that their abstraction mechanisms also require the introduction of parameters, though they may not be function parameters.

15.1 Abstractions from Examples🔗

When you first learned to add, you worked with concrete examples. Your parents probably taught you to use your fingers to add two small numbers. Later on, you studied how to add two arbitrary numbers; you were introduced to your first kind of abstraction. Much later still, you learned to formulate expressions that convert temperatures from Celsius to Fahrenheit or calculate the distance that a car travels at a given speed and amount of time. In short, you went from very concrete examples to abstract relations.

; List-of-numbers -> List-of-numbers
; converts a list of Celsius
; temperatures to Fahrenheit
(define (cf* l)
  (cond
    [(empty? l) '()]
    [else
     (cons
       (C2F (first l))
       (cf* (rest l)))]))

; Inventory -> List-of-strings
; extracts the names of
; toys from an inventory
(define (names i)
  (cond
    [(empty? i) '()]
    [else
     (cons
       (IR-name (first i))
       (names (rest i)))]))

; Number -> Number
; converts one Celsius
; temperature to Fahrenheit
(define (C2F c)
  (+ (* 9/5 c) 32))

(define-struct IR
  [name price])
; An IR is a structure:
;   (make-IR String Number)
; An Inventory is one of:
; – '()
; – (cons IR Inventory)
Figure 90: A pair of similar functions

(define (cf* l g)
  (cond
    [(empty? l) '()]
    [else
     (cons
       (g (first l))
       (cf* (rest l) g))]))

(define (names i g)
  (cond
    [(empty? i) '()]
    [else
     (cons
       (g (first i))
       (names (rest i) g))]))

(define (map1 k g)
  (cond
    [(empty? k) '()]
    [else
     (cons
       (g (first k))
       (map1 (rest k) g))]))

(define (map1 k g)
  (cond
    [(empty? k) '()]
    [else
     (cons
       (g (first k))
       (map1 (rest k) g))]))
Figure 91: The same two similar functions, abstracted

This section introduces a design recipe for creating abstractions from examples. As the preceding section shows, creating abstractions is easy. We leave the difficult part to the next section where we show you how to find and use existing abstractions.

Recall the essence of Similarities Everywhere. We start from two concrete definitions; we compare them; we mark the differences; and then we abstract. And that is mostly all there is to creating abstractions:

Step 1 is to compare two items for similarities.
When you find two function definitions that are almost the same except for their names and some valuesThe recipe requires a substantial modification for abstracting over non-values. at analogous places, compare them and mark the differences. If the two definitions differ in more than one place, connect the corresponding differences with a line.
Figure 90 shows a pair of similar function definitions. The two functions apply a function to each item in a list. They differ only as to which function they apply to each item. The two highlights emphasize this essential difference. They also differ in two inessential ways: the names of the functions and the names of the parameters.
Next we abstract. To abstract means to replace the contents of corresponding code highlights with new names and add these names to the parameter list. For our running example, we obtain the following pair of functions after replacing the differences with g; see figure 91. This first change eliminates the essential difference. Now each function traverses a list and applies some given function to each item.
The inessential differences—the names of the functions and occasionally the names of some parameters—are easy to eliminate. Indeed, if you have explored DrRacket, you know that check syntax allows you to do this systematically and easily; see bottom of figure 91. We choose to use map1 for the name of the function and k for the name of the list parameter. No matter which names you choose, the result is two identical function definitions.
Our example is simple. In many cases, you will find that there is more than just one pair of differences. The key is to find pairs of differences. When you mark up the differences with paper and pencil, connect related boxes with a line. Then introduce one additional parameter per line. And don’t forget to change all recursive uses of the function so that the additional parameters go along for the ride.

Now we must validate that the new function is a correct abstraction of the original pair of functions. To validate means to test, which here means to define the two original functions in terms of the abstraction.

Thus suppose that one original function is called f-original and consumes one argument and that the abstract function is called abstract. If f-original differs from the other concrete function in the use of one value, say, val, the following function definition

(define (f-from-abstract x)
(abstract x val))

introduces the function f-from-abstract, which should be equivalent to f-original. That is, (f-from-abstract V) should produce the same answer as (f-original V) for every proper value V. In particular, it must hold for all values that your tests for f-original use. So reformulate and rerun those tests for f-from-abstract and make sure they succeed.

Let’s return to our running example:

; List-of-numbers -> List-of-numbers
(define (cf*-from-map1 l) (map1 l C2F))

; Inventory -> List-of-strings
(define (names-from-map1 i) (map1 i IR-name))

A complete example would include some tests, and thus we can assume that both cf* and names come with some tests:

(check-expect (cf* (list 100 0 -40))
              (list 212 32 -40))

(check-expect (names
                (list
                  (make-IR "doll" 21.0)
                  (make-IR "bear" 13.0)))
              (list "doll" "bear"))

To ensure that the functions defined in terms of map1 work properly, you can copy the tests and change the function names appropriately:

(check-expect
  (cf*-from-map1 (list 100 0 -40))
                 (list 212 32 -40))

(check-expect
  (names-from-map1
    (list
      (make-IR "doll" 21.0)
      (make-IR "bear" 13.0)))
  (list "doll" "bear"))

A new abstraction needs a signature, because, as Using Abstractions explains, the reuse of abstractions starts with their signatures. Finding useful signatures is a serious problem. For now we use the running example to illustrate the difficulty; Similarities in Signatures resolves the issue.
Consider the problem of map1’s signature. On the one hand, if you view map1 as an abstraction of cf*, you might think it is
; List-of-numbers [Number -> Number] -> List-of-numbers
that is, the original signature extended with one part for functions:
; [Number -> Number]
Since the additional parameter for map1 is a function, the use of a function signature to describe it should not surprise you. This function signature is also quite simple; it is a “name” for all the functions from numbers to numbers. Here C2F is such a function, and so are add1, sin, and imag-part.
On the other hand, if you view map1 as an abstraction of names, the signature is quite different:
; Inventory [IR -> String] -> List-of-strings
This time the additional parameter is IR-name, which is a selector function that consumes IRs and produces Strings. But clearly this second signature would be useless in the first case, and vice versa. To accommodate both cases, the signature for map1 must express that Number, IR, and String are coincidental.
Also concerning signatures, you are probably eager to use List-of by now. It is clearly easier to write [List-of IR] than spelling out a data definition for Inventory. So yes, as of now, we use List-of when it is all about lists, and you should too.

Once you have abstracted two functions, you should check whether there are other uses for the abstract function. If so, the abstraction is truly useful. Consider map1, for example. It is easy to see how to use it to add 1 to each number on a list of numbers:

; List-of-numbers -> List-of-numbers
(define (add1-to-each l)
(map1 l add1))

Similarly, map1 can also be used to extract the price of each item in an inventory. When you can imagine many such uses for a new abstraction, add it to a library of useful functions to have around. Of course, it is quite likely that someone else has thought of it and the function is already a part of the language. For a function like map1, see Using Abstractions.

; Number -> [List-of Number]
; tabulates sin between n
; and 0 (incl.) in a list
(define (tab-sin n)
  (cond
    [(= n 0) (list (sin 0))]
    [else
     (cons
      (sin n)
      (tab-sin (sub1 n)))]))

; Number -> [List-of Number]
; tabulates sqrt between n
; and 0 (incl.) in a list
(define (tab-sqrt n)
  (cond
    [(= n 0) (list (sqrt 0))]
    [else
     (cons
      (sqrt n)
      (tab-sqrt (sub1 n)))]))
Figure 92: The similar functions for exercise 250

; [List-of Number] -> Number
; computes the sum of
; the numbers on l
(define (sum l)
  (cond
    [(empty? l) 0]
    [else
     (+ (first l)
        (sum (rest l)))]))

; [List-of Number] -> Number
; computes the product of
; the numbers on l
(define (product l)
  (cond
    [(empty? l) 1]
    [else
     (* (first l)
        (product (rest l)))]))
Figure 93: The similar functions for exercise 251

Exercise 250. Design tabulate, which is the abstraction of the two functions in figure 92. When tabulate is properly designed, use it to define a tabulation function for sqr and tan.

Exercise 251. Design fold1, which is the abstraction of the two functions in figure 93.

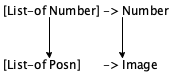
Exercise 252. Design fold2, which is the abstraction of the two functions in figure 94. Compare this exercise with exercise 251. Even though both involve the product function, this exercise poses an additional challenge because the second function, image*, consumes a list of Posns and produces an Image. Still, the solution is within reach of the material in this section, and it is especially worth comparing the solution with the one to the preceding exercise. The comparison yields interesting insights into abstract signatures.

; [List-of Number] -> Number
(define (product l)
  (cond
    [(empty? l) 1]
    [else
     (* (first l)
        (product
          (rest l)))]))

; [List-of Posn] -> Image
(define (image* l)
  (cond
    [(empty? l) emt]
    [else
     (place-dot
      (first l)
      (image* (rest l)))]))

; Posn Image -> Image
(define (place-dot p img)
  (place-image
     dot
     (posn-x p) (posn-y p)
     img))

; graphical constants:
(define emt
  (empty-scene 100 100))
(define dot
  (circle 3 "solid" "red"))
Figure 94: The similar functions for exercise 252

Lastly, when you are dealing with data definitions, the abstraction process proceeds in an analogous manner. The extra parameters to data definitions stand for collections of values, and testing means spelling out a data definition for some concrete examples. All in all, abstracting over data definitions tends to be easier than abstracting over functions, and so we leave it to you to adapt the design recipe appropriately.

15.2 Similarities in Signatures🔗

As it turns out, a function’s signature is key to its reuse. Hence, you must learn to formulate signatures that describe abstracts in their most general terms possible. To understand how this works, we start with a second look at signatures and from the simple—though possibly startling—insight that signatures are basically data definitions.

Both signatures and data definitions specify a class of data; the difference is that data definitions also name the class of data while signatures don’t. Nevertheless, when you write down

; Number Boolean -> String
(define (f n b) "hello world")

your first line describes an entire class of data, and your second one states that f belongs to that class. To be precise, the signature describes the class of all functions that consume a Number and a Boolean and yield a String.

In general, the arrow notation of signatures is like the List-of notation from Similarities in Data Definitions. The latter consumes (the name of) one class of data, say X, and describes all lists of X items—without assigning it a name. The arrow notation consumes an arbitrary number of classes of data and describes collections of functions.

What this means is that the abstraction design recipe applies to signatures, too. You compare similar signatures; you highlight the differences; and then you replace those with parameters. But the process of abstracting signatures feels more complicated than the one for functions, partly because signatures are already abstract pieces of the design recipe and partly because the arrow-based notation is much more complex than anything else we have encountered.

Let’s start with the signatures of cf* and names:

The diagram is the result of the compare-and-contrast step. Comparing the two signatures shows that they differ in two places: to the left of the arrow, we see Number versus IR, and to its right, it is Number versus String.

If we replace the two differences with some kind of parameters, say X and Y, we get the same signature:

; [X Y] [List-of X] -> [List-of Y]

The new signature starts with a sequence of variables, drawing an analogy to function definitions and the data definitions above. Roughly speaking, these variables are the parameters of the signature, like those of functions and data definitions. To make the latter concrete, the variable sequence is like ITEM in the definition of List-of or the X and Y in the definition of CP from Similarities in Data Definitions. And just like those, X and Y range over classes of values.

An instantiation of this parameter list is the rest of the signature with the parameters replaced by the data collections: either their names or other parameters or abbreviations such as List-of from above. Thus, if you replace both X and Y with Number, you get back the signature for cf*:

; [List-of Number] -> [List-of Number]

If you choose IR and String, you get back the signature for names:

; [List-of IR] -> [List-of String]

And that explains why we may consider this parametrized signature as an abstraction of the original signatures for cf* and names.

Once we add the extra function parameter to these two functions, we get map1, and the signatures are as follows:

Again, the signatures are in pictorial form and with arrows connecting the corresponding differences. These markups suggest that the differences in the second argument—a function—are related to the differences in the original signatures. Specifically, Number and IR on the left of the new arrow refer to items on the first argument—a list—and the Number and String on the right refer to the items on the result—also a list.

Since listing the parameters of a signature is extra work, for our purposes, we simply say that from now on all variables in signatures are parameters. Other programming languages, however, insist on explicitly listing the parameters of signatures, but in return you can articulate additional constraints in such signatures and the signatures are checked before you run the program.

Now let’s apply the same trick to get a signature for map1:

; [X Y] [List-of X] [X -> Y] -> [List-of Y]

Concretely, map1 consumes a list of items, all of which belong to some (yet to be determined) collection of data called X. It also consumes a function that consumes elements of X and produces elements of a second unknown collection, called Y. The result of map1 is lists that contain items from Y.

Abstracting over signatures takes practice. Here is a second pair:

; [List-of Number] -> Number
; [List-of Posn] -> Image

They are the signatures for product and image* in exercise 252. While the two signatures have some common organization, the differences are distinct. Let us first spell out the common organization in detail:

both signatures describe one-argument functions; and
both argument descriptions employ the List-of construction.

In contrast to the first example, here one signature refers to Number twice while the second one refers to Posns and Images in analogous positions. A structural comparison shows that the first occurrence of Number corresponds to Posn and the second one to Image:

To make progress on a signature for the abstraction of the two functions in exercise 252, let’s take the first two steps of the design recipe:

(define (pr* l bs jn)
  (cond
    [(empty? l) bs]
    [else
     (jn (first l)
         (pr* (rest l)
              bs
              jn))]))

(define (im* l bs jn)
  (cond
    [(empty? l) bs]
    [else
     (jn (first l)
         (im* (rest l)
              bs
              jn))]))

Since the two functions differ in two pairs of values, the revised versions consume two additional values: one is an atomic value, to be used in the base case, and the other one is a function that joins together the result of the natural recursion with the first item on the given list.

The key is to translate this insight into two signatures for the two new functions. When you do so for pr*, you get

; [List-of Number] Number [Number Number -> Number]
; -> Number

because the result in the base case is a number and because the function for the second cond line is *. Similarly, the signature for im* is

; [List-of Posn] Image [Posn Image -> Image]
; -> Image

As you can see from the function definition for im*, the base case returns an image, and the combination function is place-dot, which combines a Posn and an Image into an Image.

Now we take the diagram from above and extend it to the signatures with the additional inputs:

From this diagram, you can easily see that the two revised signatures share even more organization than the original two. Furthermore, the pieces that describe the base cases correspond to each other and so do the pieces of the sub-signature that describe the combination function. All in all there are six pairs of differences, but they boil down to just two:

some occurrences of Number correspond to Posn, and
other occurrences of Number correspond to Image.

So to abstract we need two variables, one per kind of correspondence.

Here then is the signature for fold2, the abstraction from exercise 252:

; [X Y] [List-of X] Y [X Y -> Y] -> Y

Stop! Make sure that replacing both parameters of the signature, X and Y, with Number yields the signature for pr* and that replacing the same variables with Posn and Image, respectively, yields the signature for im*.

The two examples illustrate how to find general signatures. In principle the process is just like the one for abstracting functions. Due to the informal nature of signatures, however, it cannot be checked with running examples the way code is checked. Here is a step-by-step formulation:

Given two similar function definitions, f and g, compare their signatures for similarities and differences. The goal is to discover the organization of the signature and to mark the places where one signature differs from the other. Connect the differences as pairs just like you do when you analyze function bodies.
Abstract f and g into f-abs and g-abs. That is, add parameters that eliminate the differences between f and g. Create signatures for f-abs and g-abs. Keep in mind what the new parameters originally stood for; this helps you figure out the new pieces of the signatures.
Check whether the analysis of step 1 extends to the signatures of f-abs and g-abs. If so, replace the differences with variables that range over classes of data. Once the two signatures are the same, you have a signature for the abstracted function.
Test the abstract signature. First, ensure that suitable substitutions of the variables in the abstract signature yield the signatures of f-abs and g-abs. Second, check that the generalized signature is in sync with the code. For example, if p is a new parameter and its signature is
; ... [A B -> C] ...
then p must always be applied to two arguments, the first one from A and the second one from B. And the result of an application of p is going to be a C and should be used where elements of C are expected.

As with abstracting functions, the key is to compare the concrete signatures of the examples and to determine the similarities and differences. With enough practice and intuition, you will soon be able to abstract signatures without much guidance.

Exercise 253. Each of these signatures describes a class of functions:

; [Number -> Boolean]
; [Boolean String -> Boolean]
; [Number Number Number -> Number]
; [Number -> [List-of Number]]
; [[List-of Number] -> Boolean]

Describe these collections with at least one example from ISL.

Exercise 254. Formulate signatures for the following functions:

sort-n, which consumes a list of numbers and a function that consumes two numbers (from the list) and produces a Boolean; sort-n produces a sorted list of numbers.
sort-s, which consumes a list of strings and a function that consumes two strings (from the list) and produces a Boolean; sort-s produces a sorted list of strings.

Then abstract over the two signatures, following the above steps. Also show that the generalized signature can be instantiated to describe the signature of a sort function for lists of IRs.

Exercise 255. Formulate signatures for the following functions:

map-n, which consumes a list of numbers and a function from numbers to numbers to produce a list of numbers.
map-s, which consumes a list of strings and a function from strings to strings and produces a list of strings.

Then abstract over the two signatures, following the above steps. Also show that the generalized signature can be instantiated to describe the signature of the map1 function above.

15.3 Single Point of Control🔗

In general, programs are like drafts of papers. Editing drafts is important to correct typos, to fix grammatical mistakes, to make the document consistent, and to eliminate repetitions. Nobody wants to read papers that repeat themselves a lot, and nobody wants to read such programs either.

The elimination of similarities in favor of abstractions has many advantages. Creating an abstraction simplifies definitions. It may also uncover problems with existing functions, especially when similarities aren’t quite right. But, the single most important advantage is the creation of single points of control for some common functionality.

Putting the definition for some functionality in one place makes it easy to maintain a program. When you discover a mistake, you have to go to just one place to fix it. When you discover that the code should deal with another form of data, you can add the code to just one place. When you figure out an improvement, one change improves all uses of the functionality. If you had made copies of the functions or code in general, you would have to find all copies and fix them; otherwise the mistake might live on or only one of the functions would run faster.

We therefore formulate this guideline:

Form an abstraction instead of copying and modifying any code.

Our design recipe for abstracting functions is the most basic tool to create abstractions. To use it requires practice. As you practice, you expand your capabilities to read, organize, and maintain programs. The best programmers are those who actively edit their programs to build new abstractions so that they collect things related to a task at a single point. Here we use functional abstraction to study this practice; in other courses on programming, you will encounter other forms of abstraction, most importantly inheritance in class-based object-oriented languages.

15.4 Abstractions from Templates🔗

The first two chapters of this part present many functions based on the same template. After all, the design recipe says to organize functions around the organization of the (major) input data definition. It is therefore not surprising that many function definitions look similar to each other.

Indeed, you should abstract from the templates directly, and you should do so automatically; some experimental programming languages do so. Even though this topic is still a subject of research, you are now in a position to understand the basic idea. Consider the template for lists:

(define (fun-for-l l)
  (cond
    [(empty? l) ...]
    [else (... (first l) ...
           ... (fun-for-l (rest l)) ...)]))

It contains two gaps, one in each clause. When you use this template to define a list-processing function, you usually fill these gaps with a value in the first cond clause and with a function combine in the second clause. The combine function consumes the first item of the list and the result of the natural recursion and creates the result from these two pieces of data.

Now that you know how to create abstractions, you can complete the definition of the abstraction from this informal description:

; [X Y] [List-of X] Y [X Y -> Y] -> Y
(define (reduce l base combine)
  (cond
    [(empty? l) base]
    [else (combine (first l)
                   (reduce (rest l) base combine))]))

It consumes two extra arguments: base, which is the value for the base case, and combine, which is the function that performs the value combination for the second clause.

Using reduce you can define many plain list-processing functions as “one liners.” Here are definitions for sum and product, two functions used several times in the first few sections of this chapter:

; [List-of Number] -> Number
(define (sum lon)
  (reduce lon 0 +))

; [List-of Number] -> Number
(define (product lon)
  (reduce lon 1 *))

For sum, the base case always produces 0; adding the first item and the result of the natural recursion combines the values of the second clause. Analogous reasoning explains product. Other list-processing functions can be defined in a similar manner using reduce.

16 Using Abstractions🔗

Once you have abstractions, you should use them when possible. They create single points of control, and they are a work-saving device. More precisely, the use of an abstraction helps readers of your code to understand your intentions. If the abstraction is well-known and built into the language or comes with its standard libraries, it signals more clearly what your function does than custom-designed code.

This chapter is all about the reuse of existing ISL abstractions. It starts with a section on existing ISL abstractions, some of which you have seen under false names. The remaining sections are about reusing such abstractions. One key ingredient is a new syntactic construct, local, for defining functions and variables (and even structure types) locally within a function. An auxiliary ingredient, introduced in the last section, is the lambda construct for creating nameless functions; lambda is a convenience but inessential to the idea of reusing abstract functions.

; [X] N [N -> X] -> [List-of X]
; constructs a list by applying f to 0, 1, ..., (sub1 n)
; (build-list n f) == (list (f 0) ... (f (- n 1)))
(define (build-list n f) ...)

; [X] [X -> Boolean] [List-of X] -> [List-of X]
; produces a list from those items on lx for which p holds
(define (filter p lx) ...)

; [X] [List-of X] [X X -> Boolean] -> [List-of X]
; produces a version of lx that is sorted according to cmp
(define (sort lx cmp) ...)

; [X Y] [X -> Y] [List-of X] -> [List-of Y]
; constructs a list by applying f to each item on lx
; (map f (list x-1 ... x-n)) == (list (f x-1) ... (f x-n))
(define (map f lx) ...)

; [X] [X -> Boolean] [List-of X] -> Boolean
; determines whether p holds for every item on lx
; (andmap p (list x-1 ... x-n)) == (and (p x-1) ... (p x-n))
(define (andmap p lx) ...)

; [X] [X -> Boolean] [List-of X] -> Boolean
; determines whether p holds for at least one item on lx
; (ormap p (list x-1 ... x-n)) == (or (p x-1) ... (p x-n))
(define (ormap p lx) ...)
Figure 95: ISL’s abstract functions for list processing (1)

16.1 Existing Abstractions🔗

ISL provides a number of abstract functions for processing natural numbers and lists. Figure 95 collects the header material for the most important ones. The first one processes natural numbers and builds lists:

> (build-list 3 add1)
(list 1 2 3)

The next three process lists and produce lists:

> (filter odd? (list 1 2 3 4 5))
(list 1 3 5)
> (sort (list 3 2 1 4 5) >)
(list 5 4 3 2 1)
> (map add1 (list 1 2 2 3 3 3))
(list 2 3 3 4 4 4)

In contrast, andmap and ormap reduce lists to a Boolean:

> (andmap odd? (list 1 2 3 4 5))
#false
> (ormap odd? (list 1 2 3 4 5))
#true

Hence, this kind of computation is called a reduction.

; [X Y] [X Y -> Y] Y [List-of X] -> Y
; applies f from right to left to each item in lx and b
; (foldr f b (list x-1 ... x-n)) == (f x-1 ... (f x-n b))
(define (foldr f b lx) ...)

(foldr + 0 '(1 2 3 4 5))
== (+ 1 (+ 2 (+ 3 (+ 4 (+ 5 0)))))
== (+ 1 (+ 2 (+ 3 (+ 4 5))))
== (+ 1 (+ 2 (+ 3 9)))
== (+ 1 (+ 2 12))
== (+ 1 14)

; [X Y] [X Y -> Y] Y [List-of X] -> Y
; applies f from left to right to each item in lx and b
; (foldl f b (list x-1 ... x-n)) == (f x-n ... (f x-1 b))
(define (foldl f b lx) ...)

(foldl + 0 '(1 2 3 4 5))
== (+ 5 (+ 4 (+ 3 (+ 2 (+ 1 0)))))
== (+ 5 (+ 4 (+ 3 (+ 2 1))))
== (+ 5 (+ 4 (+ 3 3)))
== (+ 5 (+ 4 6))
== (+ 5 10)
Figure 96: ISL’s abstract functions for list processing (2)

The two functions in figure 96, foldr and foldl, are extremely powerful. Both reduce lists to values. The sample computations explain the abstract examples in the headers of foldr and foldl via an application of the functions to +, 0, and a short list. As you canMathematics calls functions associative if the order makes no difference. ISL’s = is associative on integers but not on inexacts. See below. see, foldr processes the list values from right to left and foldl from left to right. While for some functions the direction makes no difference, this isn’t true in general.

Exercise 256. Explain the following abstract function:

; [X] [X -> Number] [NEList-of X] -> X
; finds the (first) item in lx that maximizes f
; if (argmax f (list x-1 ... x-n)) == x-i,
; then (>= (f x-i) (f x-1)), (>= (f x-i) (f x-2)), ...
(define (argmax f lx) ...)

Use it on concrete examples in ISL. Can you articulate an analogous purpose statement for argmin?

(define-struct address [first-name last-name street])
; An Addr is a structure:
;   (make-address String String String)
; interpretation associates an address with a person's name

; [List-of Addr] -> String
; creates a string from first names,
; sorted in alphabetical order,
; separated and surrounded by blank spaces
(define (listing l)
  (foldr string-append-with-space " "
         (sort (map address-first-name l) string<?)))

; String String -> String
; appends two strings, prefixes with " "
(define (string-append-with-space s t)
  (string-append " " s t))

(define ex0
  (list (make-address "Robert"   "Findler" "South")
        (make-address "Matthew"  "Flatt"   "Canyon")
        (make-address "Shriram"  "Krishna" "Yellow")))

(check-expect (listing ex0) " Matthew Robert Shriram ")
Figure 97: Creating a program with abstractions

Figure 97 illustrates the power of composing the functions from figures 95 and 96. Its main function is listing. The purpose is to create a string from a list of addresses. Its purpose statement suggests three tasks and thus the design of three functions:

one that extracts the first names from the given list of Addr;
one that sorts these names in alphabetical order; and
one that concatenates the strings from step 2.

Before you read on, you may wish to execute this plan. That is, design all three functions and then compose them in the sense of Composing Functions to obtain your own version of listing.

In the new world of abstractions, it is possible to design a single function that achieves the same goal. Take a close look at the innermost expression of listing in figure 97:

(map address-first-name l)

By the purpose statement of map, it applies address-first-name to every single instance of address, producing a list of first names as strings. Here is the immediately surrounding expression:

(sort ... string<?)

The dots represent the result of the map expression. Since the latter supplies a list of strings, the sort expression produces a sorted list of first names. And that leaves us with the outermost expression:

(foldr string-append-with-space " " ...)

This one reduces the sorted list of first names to a single string, using a function named string-append-with-space. With such a suggestive name, you can easily imagine now that this reduction concatenates all the strings in the desired way—even if you do not quite understand how the combination of foldr and string-append-with-space works.

Exercise 257. You can design build-list and foldl with the design recipes that you know, but they are not going to be like the ones that ISL provides. For example, the design of your own foldl function requires a use of the list reverse function:

; [X Y] [X Y -> Y] Y [List-of X] -> Y
; f*oldl works just like foldl
(check-expect (f*oldl cons '() '(a b c))
              (foldl cons '() '(a b c)))
(check-expect (f*oldl / 1 '(6 3 2))
              (foldl / 1 '(6 3 2)))
(define (f*oldl f e l)
  (foldr f e (reverse l)))

Design build-l*st, which works just like build-list. Hint Recall the add-at-end function from exercise 193. Note on Design Accumulators covers the concepts needed to design these functions from scratch.

16.2 Local Definitions🔗

Let’s take a second look at figure 97. The string-append-with-space function clearly plays a subordinate role and has no use outside of this narrow context. Furthermore, the organization of the function body does not reflect the three tasks identified above.

Almost all programming languages support some way for stating these kinds of relationships as a part of a program. The idea is called a local definition, also called a private definition. In ISL, local expressions introduce locally defined functions, variables, and structure types.

This section introduces the mechanics of local. In general, a local expression has this shape:

(local (def ...)
; — IN —
body-expression)

The evaluation of such an expression proceeds like the evaluation of a complete program. First, the definitions are set up, which may involve the evaluation of the right-hand side of a constant definition. Just as with the top-level definitions that you know and love, the definitions in a local expression may refer to each other. They may also refer to parameters of the surrounding function. Second, the body-expression is evaluated and it becomes the result of the local expression. It is often helpful to separate the local defs from the body-expression with a comment; as indicated, we may use — IN — because the word suggests that the definitions are available in a certain expression.

; [List-of Addr] -> String
; creates a string of first names,
; sorted in alphabetical order,
; separated and surrounded by blank spaces
(define (listing.v2 l)
  (local (; 1. extract names
          (define names  (map address-first-name l))
          ; 2. sort the names
          (define sorted (sort names string<?))
          ; 3. append them, add spaces
          ; String String -> String
          ; appends two strings, prefix with " "
          (define (helper s t)
            (string-append " " s t))
          (define concat+spaces
            (foldr helper " " sorted)))
    concat+spaces))
Figure 98: Organizing a function with local

Figure 98 shows a revision of figure 97 using local. The body of the listing.v2 function is now a local expression, which consists of two pieces: a sequence of definitions and a body expression. The sequence of local definitions looks exactly like a sequence in DrRacket’s definitions area.

In this example, the sequence of definitions consists of four pieces: three constant definitions and a single function definition. Each constant definition represents one of the three planning tasks. The function definition is a renamed versionSince the names are visible only within the local expression, shortening the name is fine. of string-append-with-space; it is used with foldr to implement the third task. The body of local is just the name of the third task.

The visually most appealing difference concerns the overall organization. It clearly brings across that the function achieves three tasks and in which order. As a matter of fact, this example demonstrates a general principle of readability:

Use local to reformulate deeply nested expressions. Use well-chosen names to express what the expressions compute.

Future readers appreciate it because they can comprehend the code by looking at just the names and the body of the local expression.

Note on Organization A local expression is really just an expression. It may show up wherever a regular expression shows up. Hence it is possible to indicate precisely where an auxiliary function is needed. Consider this reorganization of the local expression of listing.v2:

... (local ((define names  ...)
            (define sorted ...)
            (define concat+spaces
              (local (; String String -> String
                      (define (helper s t)
                        (string-append " " s t)))
                (foldr helper " " sorted))))
      concat+spaces) ...

It consists of exactly three definitions, suggesting it takes three computation steps. The third definition consists of a local expression on the right-hand side, which expresses that helper is really just needed for the third step.

Whether you want to express relationships among the pieces of a program with such precision depends on two constraints: the programming language and how long the code is expected to live. Some languages cannot even express the idea that helper is useful for the third step only. Then again, you need to balance the time it takes to create the program and the expectation that you or someone needs to revisit it and comprehend the code again. The preference of the Racket team is to err on the side of future developers because the team members know that no program is ever finished and all programs will need fixing. End

; [List-of Number] [Number Number -> Boolean]
; -> [List-of Number]
; produces a version of alon0, sorted according to cmp
(define (sort-cmp alon0 cmp)
  (local (; [List-of Number] -> [List-of Number]
          ; produces the sorted version of alon
          (define (isort alon)
            (cond
              [(empty? alon) '()]
              [else
               (insert (first alon) (isort (rest alon)))]))

          ; Number [List-of Number] -> [List-of Number]
          ; inserts n into the sorted list of numbers alon
          (define (insert n alon)
            (cond
              [(empty? alon) (cons n '())]
              [else (if (cmp n (first alon))
                        (cons n alon)
                        (cons (first alon)
                              (insert n (rest alon))))])))
    (isort alon0)))
Figure 99: Organizing interconnected function definitions with local

Figure 99 presents a second example. The organization of this function definition informs the reader that sort-cmp calls on two auxiliary functions: isort and insert. By locality, it becomes obvious that the adjective “sorted” in the purpose statement of insert refers to isort. In other words, insert is useful in this context only; a programmer should not try to use it elsewhere, out of context. While this constraint is already important in the original definition of the sort-cmp function, a local expression expresses it as part of the program.

Another important aspect of this reorganization of sort-cmp’s definition concerns the visibility of cmp, the second function parameter. The locally defined functions can refer to cmp because it is defined in the context of the definitions. By not passing around cmp from isort to insert (or back), the reader can immediately infer that cmp remains the same throughout the sorting process.

Exercise 258. Use a local expression to organize the functions for drawing a polygon in figure 73. If a globally defined function is widely useful, do not make it local.

Exercise 259. Use a local expression to organize the functions for rearranging words from Word Games, the Heart of the Problem.

; Nelon -> Number
; determines the smallest number on l
(define (inf.v2 l)
  (cond
    [(empty? (rest l)) (first l)]
    [else
     (local ((define smallest-in-rest (inf.v2 (rest l))))
       (if (< (first l) smallest-in-rest)
           (first l)
           smallest-in-rest))]))
Figure 100: Using local may improve performance

Our final example of local’s usefulness concerns performance. Consider the definition of inf in figure 89. It contains two copies of

(inf (rest l))

which is the natural recursion in the second cond line. Depending on the outcome of the question, the expression is evaluated twice. Using local to name this expression yields an improvement to the function’s readability as well as to its performance.

Figure 100 displays the revised version. Here the local expression shows up in the middle of a cond expression. It defines a constant whose value is the result of a natural recursion. Now recall that the evaluation of a local expression evaluates the definitions once before proceeding to the body, meaning (inf (rest l)) is evaluated once while the body of the local expression refers to the result twice. Thus, local saves the re-evaluation of (inf (rest l)) at each stage in the computation.

Exercise 260. Confirm the insight about the performance of inf.v2 by repeating the performance experiment of exercise 238.

; Inventory -> Inventory
; creates an Inventory from an-inv for all
; those items that cost less than a dollar
(define (extract1 an-inv)
  (cond
    [(empty? an-inv) '()]
    [else
     (cond
       [(<= (IR-price (first an-inv)) 1.0)
        (cons (first an-inv) (extract1 (rest an-inv)))]
       [else (extract1 (rest an-inv))])]))
Figure 101: A function on inventories, see exercise 261

Exercise 261. Consider the function definition in figure 101. Both clauses in the nested cond expression extract the first item from an-inv and both compute (extract1 (rest an-inv)). Use local to name this expression. Does this help increase the speed at which the function computes its result? Significantly? A little bit? Not at all?

16.3 Local Definitions Add Expressive Power🔗

The third and last example illustrates how local adds expressive power to BSL and BSL+. Finite State Machines presents the design of a world program that simulates how a finite state machine recognizes sequences of keystrokes. While the data analysis leads in a natural manner to the data definitions in figure 82, an attempt to design the main function of the world program fails. Specifically, even though the given finite state machine remains the same over the course of the simulation, the state of the world must include it so that the program can transition from one state to the next when the player presses a key.

; FSM FSM-State -> FSM-State
; matches the keys pressed by a player with the given FSM
(define (simulate fsm s0)
  (local (; State of the World: FSM-State
          ; FSM-State KeyEvent -> FSM-State
          (define (find-next-state s key-event)
            (find fsm s)))
    (big-bang s0
      [to-draw state-as-colored-square]
      [on-key find-next-state])))

; FSM-State -> Image
; renders current state as colored square
(define (state-as-colored-square s)
  (square 100 "solid" s))

; FSM FSM-State -> FSM-State
; finds the current state's successor in fsm
(define (find transitions current)
  (cond
    [(empty? transitions) (error "not found")]
    [else
      (local ((define s (first transitions)))
        (if (state=? (transition-current s) current)
            (transition-next s)
            (find (rest transitions) current)))]))
Figure 102: Power from local function definitions

Figure 102 shows an ISL solution to the problem. It uses local function definitions and can thus equate the state of the world with the current state of the finite state machine. Specifically, simulate locally defines the key-event handler, which consumes only the current state of the world and the KeyEvent that represents the player’s keystroke. Because this locally defined function can refer to the given finite state machine fsm, it is possible to find the next state in the transition table—even though the transition table is not an argument to this function.

As the figure also shows, all other functions are defined in parallel to the main function. This includes the function find, which performs the actual search in the transition table. The key improvement over BSL is that a locally defined function can reference both parameters to the function and globally defined auxiliary functions.

In short, this program organization signals to a future reader exactly the insights that the data analysis stage of the design recipe for world programs finds. First, the given representation of the finite state machine remains unchanged. Second, what changes over the course of the simulation is the current state of the finite machine.

The lesson is that the chosen programming language affects a programmer’s ability to express solutions, as well as a future reader’s ability to recognize the design insight of the original creator.

Exercise 262. Design the function identityM, which creates diagonal squares of 0s and 1s:Linear algebra calls these squares identity matrices.

> (identityM 1)
(list (list 1))
> (identityM 3)
(list (list 1 0 0) (list 0 1 0) (list 0 0 1))

Use the structural design recipe and exploit the power of local.

16.4 Computing with local🔗

ISL’s local expression calls for the first rule of calculation that is truly beyond pre-algebra knowledge. The rule is relatively simple but quite unusual. It’s best illustrated with some examples. We start with a second look at this definition:

(define (simulate fsm s0)
  (local ((define (find-next-state s key-event)
            (find fsm s)))
    (big-bang s0
      [to-draw state-as-colored-square]
      [on-key find-next-state])))

Now suppose we wish to calculate what DrRacket might produce for

(simulate AN-FSM A-STATE)

where AN-FSM and A-STATE are unknown values. Using the usual substitution rule, we proceed as follows:

==
(local ((define (find-next-state s key-event)
          (find AN-FSM s)))
  (big-bang A-STATE
    [to-draw state-as-colored-square]
    [on-key find-next-state]))

This is the body of simulate with all occurrences of fsm and s0 replaced by the argument values AN-FSM and A-STATE, respectively.

At this point we are stuck because the expression is a local expression, and we don’t know how to calculate with it. So here we go. To deal with a local expression in a program evaluation, we proceed in two steps:

We rename the locally defined constants and functions to use names that aren’t used elsewhere in the program.
We lift the definitions in the local expression to the top level and evaluate the body of the local expression next.

Stop! Don’t think. Accept the two steps for now.

Let’s apply these two steps to our running example, one at a time:

==
(local ((define (find-next-state-1 s key-event)
          (find AN-FSM a-state)))
  (big-bang A-STATE
    [to-draw state-as-colored-square]
    [on-key find-next-state-1]))

Our choice is to append “-1” to the end of the function name. If this variant of the name already exists, we use “-2” instead, and so on. So here is the result of step 2: We use

to indicate that the step produces two pieces.

==
(define (find-next-state-1 s key-event)
   (find AN-FSM a-state))
(big-bang A-STATE
  [to-draw state-as-colored-square]
  [on-key find-next-state-1])

The result is an ordinary program: some globally defined constants and functions followed by an expression. The normal rules apply, and there is nothing else to say.

At this point, it is time to rationalize the two steps. For the renaming step, we use a variant of the inf function from figure 100. Clearly,

(inf (list 2 1 3)) == 1

The question is whether you can show the calculations that DrRacket performs to determine this result.

The first step is straightforward:

(inf (list 2 1 3))
==
(cond
  [(empty? (rest (list 2 1 3)))
   (first (list 2 1 3))]
  [else
   (local ((define smallest-in-rest
             (inf (rest (list 2 1 3)))))
     (cond
       [(< (first (list 2 1 3)) smallest-in-rest)
        (first (list 2 1 3))]
       [else smallest-in-rest]))])

We substitute (list 2 1 3) for l.

Since the list isn’t empty, we skip the steps for evaluating the conditional and focus on the next expression to be evaluated:

...
==
(local ((define smallest-in-rest
          (inf (rest (list 2 1 3)))))
  (cond
    [(< (first (list 2 1 3)) smallest-in-rest)
     (first (list 2 1 3))]
    [else smallest-in-rest]))

Applying the two steps for the rule of local yields two parts: the local definition lifted to the top and the body of the local expression. Here is how we write this down:

==
(define smallest-in-rest-1
  (inf (rest (list 2 1 3))))
(cond
  [(< (first (list 2 1 3)) smallest-in-rest-1)
   (first (list 2 1 3))]
  [else smallest-in-rest-1])

Curiously, the next expression we need to evaluate is the right-hand side of a constant definition in a local expression. But the point of computing is that you can replace expressions with their equivalents wherever you want:

==
(define smallest-in-rest-1
  (cond
    [(empty? (rest (list 1 3))) (first (list 1 3))]
    [else
     (local ((define smallest-in-rest
               (inf (rest (list 1 3)))))
       (cond
         [(< (first (list 1 3)) smallest-in-rest)
          (first (list 1 3))]
         [else smallest-in-rest]))]))
(cond
  [(< (first (list 2 1 3)) smallest-in-rest-1)
   (first (list 2 1 3))]
  [else smallest-in-rest-1])

Once again, we skip the conditional steps and focus on the else clause, which is also a local expression. Indeed it is another variant of the local expression in the definition of inf, with a different list value substituted for the parameter:

(define smallest-in-rest-1
  (local ((define smallest-in-rest
            (inf (rest (list 1 3)))))
    (cond
      [(< (first (list 1 3)) smallest-in-rest)
       (first (list 1 3))]
      [else smallest-in-rest])))
(cond
  [(< (first (list 2 1 3)) smallest-in-rest-1)
   (first (list 2 1 3))]
  [else smallest-in-rest-3])

Because it originates from the same local expression in inf, it uses the same name for the constant, smallest-in-rest. If we didn’t rename local definitions before lifting them, we would introduce two conflicting definitions for the same name, and conflicting definitions are catastrophic for mathematical calculations.

Here is how we continue:

==
(define smallest-in-rest-2
  (inf (rest (list 1 3))))
(define smallest-in-rest-1
  (cond
    [(< (first (list 1 3)) smallest-in-rest-2)
     (first (list 1 3))]
    [else smallest-in-rest-2]))
(cond
  [(< (first (list 2 1 3)) smallest-in-rest-1)
   (first (list 2 1 3))]
  [else smallest-in-rest-1])

The key is that we now have two definitions generated from one and the same local expression in the function definition. As a matter of fact we get one such definition per item in the given list (minus 1).

Exercise 263. Use DrRacket’s stepper to study the steps of this calculation in detail.

Exercise 264. Use DrRacket’s stepper to calculate out how it evaluates

(sup (list 2 1 3))

where sup is the function from figure 89 equipped with local.

This passage and some of the following exercises already need the “Intermediate Student with lambda” language. In DrRacket, choose the corresponding entry from the “How to Design Programs” submenu in the “Language” menu.

For the explanation of the lifting step, we use a toy example that gets to the heart of the issue, namely, that functions are now values:

((local ((define (f x) (+ (* 4 (sqr x)) 3))) f)
1)

Deep down we know that this is equivalent to (f 1) where

(define (f x) (+ (* 4 (sqr x)) 3))

but the rules of pre-algebra don’t apply. The key is that functions can be the result of expressions, including local expressions. And the best way to think of this is to move such local definitions to the top and to deal with them like ordinary definitions. Doing so renders the definition visible for every step of the calculation. By now you also understand that the renaming step makes sure that the lifting of definitions does not accidentally conflate names or introduce conflicting definitions.

Here are the first two steps of the calculation:

((local ((define (f x) (+ (* 4 (sqr x)) 3))) f)
1)
==
((local ((define (f-1 x) (+ (* 4 (sqr x)) 3)))
f-1)
1)
==
(define (f-1 x) (+ (* 4 (sqr x)) 3))
(f-1 1)

Remember that the second step of the local rule replaces the local expression with its body. In this case, the body is just the name of the function, and its surrounding is an application to 1. The rest is arithmetic:

(f-1 1) == (+ (* 4 (sqr 1)) 3) == 7

Exercise 265. Use DrRacket’s stepper to fill in any gaps above.

Exercise 266. Use DrRacket’s stepper to find out how ISL evaluates

((local ((define (f x) (+ x 3))
         (define (g x) (* x 4)))
   (if (odd? (f (g 1)))
       f
       g))
2)

to 5.

16.5 Using Abstractions, by Example🔗

Now that you understand local, you can easily use the abstractions from figures 95 and 96. Let’s look at examples, starting with this one:

Sample Problem Design add-3-to-all. The function consumes a list of Posns and adds 3 to the x-coordinates of each.

If we follow the design recipe and take the problem statement as a purpose statement, we can quickly step through the first three steps:

; [List-of Posn] -> [List-of Posn]
; adds 3 to each x-coordinate on the given list

(check-expect
(add-3-to-all
(list (make-posn 3 1) (make-posn 0 0)))
(list (make-posn 6 1) (make-posn 3 0)))

(define (add-3-to-all lop) '())

While you can run the program, doing so signals a failure in the one test case because the function returns the default value '().

At this point, we stop and ask what kind of function we are dealing with. Clearly, add-3-to-all is a list-processing function. The question is whether it is like any of the functions in figures 95 and 96. The signature tells us that add-3-to-all is a list-processing function that consumes and produces a list. In the two figures, we have several functions with similar signatures: map, filter, and sort.

The purpose statement and example also tell you that add-3-to-all deals with each Posn separately and assembles the results into a single list. Some reflection also confirms that the resulting list contains as many items as the given list. All this thinking points to one function—map—because the point of filter is to drop items from the list and sort has an extremely specific purpose.

Here is map’s signature again:

; [X Y] [X -> Y] [List-of X] -> [List-of Y]

It tells us that map consumes a function from X to Y and a list of Xs. Given that add-3-to-all consumes a list of Posns, we know that X stands for Posn. Similarly, add-3-to-all is to produce a list of Posns, and this means we replace Y with Posn.

From the analysis of the signature, we conclude that map can do the job of add-3-to-all when given the right function from Posns to Posns. With local, we can express this idea as a template for add-3-to-all:

(define (add-3-to-all lop)
  (local (; Posn -> Posn
          ; ...
          (define (fp p)
            ... p ...))
    (map fp lop)))

Doing so reduces the problem to defining a function on Posns.

Given the example for add-3-to-all and the abstract example for map, you can actually imagine how the evaluation proceeds:

(add-3-to-all (list (make-posn 3 1) (make-posn 0 0)))
==
(map fp (list (make-posn 3 1) (make-posn 0 0)))
==
(list (fp (make-posn 3 1)) (fp (make-posn 0 0)))

And that shows how fp is applied to every single Posn on the given list, meaning it is its job to add 3 to the x-coordinate.

From here, it is straightforward to wrap up the definition:

(define (add-3-to-all lop)
  (local (; Posn -> Posn
          ; adds 3 to the x-coordinate of p
          (define (add-3-to-x p)
            (make-posn (+ (posn-x p) 3) (posn-y p))))
    (map add-3-to-x lop)))

We chose add-3-to-x as the name for the local function because the name tells you what it computes. It adds 3 to the x-coordinate of one Posn.

You may now think that using abstractions is hard. Keep in mind, though, that this first example spells out every single detail and that it does so because we wish to teach you how to pick the proper abstraction. Let’s take a look at a second example a bit more quickly:

Sample Problem Design a function that eliminates all Posns with y-coordinates larger than 100 from some given list.

The first three steps of the design recipe yield this:

; [List-of Posn] -> [List-of Posn]
; eliminates Posns whose y-coordinate is > 100

(check-expect
(keep-good (list (make-posn 0 110) (make-posn 0 60)))
(list (make-posn 0 60)))

(define (keep-good lop) '())

By now you may have guessed that this function is like filter, whose purpose is to separate the “good” from the “bad.”

With local thrown in, the next step is also straightforward:

(define (keep-good lop)
  (local (; Posn -> Boolean
          ; should this Posn stay on the list
          (define (good? p) #true))
    (filter good? lop)))

The local function definition introduces the helper function needed for filter, and the body of the local expression applies filter to this local function and the given list. The local function is called good? because filter retains all those items of lop for which good? produces #true.

Before you read on, analyze the signature of filter and keep-good and determine why the helper function consumes individual Posns and produces Booleans.

Putting all of our ideas together yields this definition:

(define (keep-good lop)
  (local (; Posn -> Posn
          ; should this Posn stay on the list
          (define (good? p)
            (not (> (posn-y p) 100))))
    (filter good? lop)))

Explain the definition of good? and simplify it.

Before we spell out a design recipe, let’s deal with one more example:

Sample Problem Design a function that determines whether any of a list of Posns is close to some given position pt where “close” means a distance of at most 5 pixels.

This problem clearly consists of two distinct parts: one concerns processing the list and the other one calls for a function that determines whether the distance between a point and pt is “close.” Since this second part is unrelated to the reuse of abstractions for list traversals, we assume the existence of an appropriate function:

; Posn Posn Number -> Boolean
; is the distance between p and q less than d
(define (close-to? p q d) ...)

You should complete this definition on your own.

As required by the problem statement, the function consumes two arguments: the list of Posns and the “given” point pt. It produces a Boolean:

; [List-of Posn] Posn -> Boolean
; is any Posn on lop close to pt

(check-expect
(close? (list (make-posn 47 54) (make-posn 0 60))
(make-posn 50 50))
#true)

(define (close? lop pt) #false)

The signature differentiates this example from the preceding ones.

The Boolean range also gives away a clue with respect to figures 95 and 96. Only two functions in this list produce Boolean values—andmap and ormap—and they must be primary candidates for defining close?’s body. While the explanation of andmap says that some property must hold for every item on the given list, the purpose statement for ormap tells us that it looks for only one such item. Given that close? just checks whether one of the Posns is close to pt, we should try ormap first.

Let’s apply our standard “trick” of adding a local whose body uses the chosen abstraction on some locally defined function and the given list:

(define (close? lop pt)
  (local (; Posn -> Boolean
          ; ...
          (define (is-one-close? p)
            ...))
    (ormap is-one-close? lop)))

Following the description of ormap, the local function consumes one item of the list at a time. This accounts for the Posn part of its signature. Also, the local function is expected to produce #true or #false, and ormap checks these results until it finds #true.

Here is a comparison of the signature of ormap and close?, starting with the former:

; [X] [X -> Boolean] [List-of X] -> Boolean

In our case, the list argument is a list of Posns. Hence X stands for Posn, which explains what is-one-close? consumes. Furthermore, it determines that the result of the local function must be Boolean so that it can work as the first argument to ormap.

The rest of the work requires just a bit more thinking. While is-one-close? consumes one argument—a Posn—the close-to? function consumes three: two Posns and a “tolerance” value. While the argument of is-one-close? is one of the two Posns, it is also obvious that the other one is pt, the argument of close? itself. Naturally the “tolerance” argument is 5, as stated in the problem:

(define (close? lop pt)
  (local (; Posn -> Boolean
          ; is one shot close to pt
          (define (is-one-close? p)
            (close-to? p pt CLOSENESS)))
    (ormap is-one-close? lop)))

(define CLOSENESS 5) ; in terms of pixels

Note two properties of this definition. First, we stick to the rule that constants deserve definitions. Second, the reference to pt in is-one-close? signals that this Posn stays the same for the entire traversal of lop.

16.6 Designing with Abstractions🔗

The three sample problems from the preceding section suffice for formulating a design recipe:

Step 1 is to follow the design recipe for functions for three steps. Specifically, you should distill the problem statement into a signature, a purpose statement, an example, and a stub definition.

Consider the problem of defining a function that places small red circles on a

canvas for a given list of Posns. The first three steps of the design recipe yields this much:

; [List-of Posn] -> Image
; adds the Posns on lop to the empty scene

(check-expect (dots (list (make-posn 12 31)))
(place-image DOT 12 31 MT-SCENE))

(define (dots lop)
MT-SCENE)

Add definitions for the constants so DrRacket can run the code.

Next we exploit the signature and purpose statement to find a matching abstraction. To match means to pick an abstraction whose purpose is more general than the one for the function to be designed; it also means that the signatures are related. It is often best to start with the desired output and to find an abstraction that has the same or a more general output.
For our running example, the desired output is an Image. While none of the available abstractions produces an image, two of them have a variable to the right of ->:
; foldr : [X Y] [X Y -> Y] Y [List-of X] -> Y
; foldl : [X Y] [X Y -> Y] Y [List-of X] -> Y
meaning we can plug in any data collection we want. If we do use Image, the signature on the left of -> demands a helper function that consumes an X together with an Image and produces an Image. Furthermore, since the given list contains Posns, X does stand for the Posn collection.
Write down a template. For the reuse of abstractions, a template uses local for two different purposes. The first one is to note which abstraction to use, and how, in the body of the local expression. The second one is to write down a stub for the helper function: its signature, its purpose (optionally), and its header. Keep in mind that the signature comparison in the preceding step suggests most of the signature for the auxiliary function.
Here is what this template looks like for our running example if we choose the foldr function:
(define (dots lop)
  (local (; Posn Image -> Image
          (define (add-one-dot p scene) ...))
    (foldr add-one-dot MT-SCENE lop)))
The foldr description calls for a “base” Image value, to be used if or when the list is empty. In our case, we clearly want the empty canvas for this case. Otherwise, foldr uses a helper function and traverses the list of Posns.

Finally, it is time to define the auxiliary function inside local. In most cases, this function consumes relatively simple kinds of data, like those encountered in Fixed-Size Data. You know how to design those in principle. The difference is that now you use not only the function’s arguments and global constants but also the arguments of the surrounding function.

In our running example, the purpose of the helper function is to add one dot to the given scene, which you can (1) guess or (2) derive from the example:

(define (dots lop)
  (local (; Posn Image -> Image
          ; adds a DOT at p to scene
          (define (add-one-dot p scene)
            (place-image DOT
                         (posn-x p) (posn-y p)
                         scene)))
    (foldr add-one-dot MT-SCENE lop)))

The last step is to test the definition in the usual manner.
For abstract functions, it is occasionally possible to use the abstract example of their purpose statement to confirm their workings at a more general level. You may wish to use the abstract example for foldr to confirm that dots does add one dot after another to the background scene.

In the third step, we picked foldr without further ado. Experiment with foldl to see how it would help complete this function. Functions like foldl and foldr are well-known and are spreading in usage in various forms. Becoming familiar with them is a good idea, and that’s the point of the next two sections.

16.7 Finger Exercises: Abstraction🔗

Some of these exercises already need the “Intermediate Student with lambda” language. In DrRacket, choose the corresponding entry from the “How to Design Programs” submenu in the “Language” menu.

Exercise 267. Use map to define the function convert-euro, which converts a list of US$ amounts into a list of € amounts based on an exchange rate of US$1.06 per € (on April 13, 2017).

Also use map to define convertFC, which converts a list of Fahrenheit measurements to a list of Celsius measurements.

Finally, try your hand at translate, a function that translates a list of Posns into a list of lists of pairs of numbers.

Exercise 268. An inventory record specifies the name of an item, a description, the acquisition price, and the recommended sales price.

Define a function that sorts a list of inventory records by the difference between the two prices.

Exercise 269. Define eliminate-expensive. The function consumes a number, ua, and a list of inventory records, and it produces a list of all those structures whose sales price is below ua.

Then use filter to define recall, which consumes the name of an inventory item, called ty, and a list of inventory records and which produces a list of inventory records that do not use the name ty.

In addition, define selection, which consumes two lists of names and selects all those from the second one that are also on the first.

Exercise 270. Use build-list to define a function that

creates the list (list 0 ... (- n 1)) for any natural number n;
creates the list (list 1 ... n) for any natural number n;
creates the list (list 1 1/2 ... 1/n) for any natural number n;
creates the list of the first n even numbers; and
creates a diagonal square of 0s and 1s; see exercise 262.

Finally, define tabulate from exercise 250 using build-list.

Exercise 271. Use ormap to define find-name. The function consumes a name and a list of names. It determines whether any of the names on the latter are equal to or an extension of the former.

With andmap you can define a function that checks all names on a list of names that start with the letter "a".

Should you use ormap or andmap to define a function that ensures that no name on some list exceeds a given width?

Exercise 272. Recall that the append function in ISL concatenates the items of two lists or, equivalently, replaces '() at the end of the first list with the second list:

(equal? (append (list 1 2 3) (list 4 5 6 7 8))
(list 1 2 3 4 5 6 7 8))

Use foldr to define append-from-fold. What happens if you replace foldr with foldl?

Now use one of the fold functions to define functions that compute the sum and the product, respectively, of a list of numbers.

With one of the fold functions, you can define a function that horizontally composes a list of Images. Hints (1) Look up beside and empty-image. Can you use the other fold function? Also define a function that stacks a list of images vertically. (2) Check for above in the teac=hoacks.

Exercise 273. The fold functions are so powerful that you can define almost any list processing functions with them. Use fold to define map.

Exercise 274. Use existing abstractions to define the prefixes and suffixes functions from exercise 190. Ensure that they pass the same tests as the original function.

16.8 Projects: Abstraction🔗

Now that you have some experience with the existing list-processing abstractions in ISL, it is time to tackle some of the small projects for which you already have programs. The challenge is to look for two kinds of improvements. First, inspect the programs for functions that traverse lists. For these functions, you already have signatures, purpose statements, tests, and working definitions that pass the tests. Change the definitions to use abstractions from figures 95 and 96. Second, also determine whether there are opportunities to create new abstractions. Indeed, you might be able to abstract across these classes of programs and provide generalized functions that help you write additional programs.

Exercise 275. Real-World Data: Dictionaries deals withYou may wish to tackle these exercises again after studying Nameless Functions. relatively simple tasks relating to English dictionaries. The design of two of them just call out for the use of existing abstractions:

Design most-frequent. The function consumes a Dictionary and produces the Letter-Count for the letter that is most frequently used as the first one in the words of the given Dictionary.
Design words-by-first-letter. The function consumes a Dictionary and produces a list of Dictionarys, one per Letter. Do not include '() if there are no words for some letter; ignore the empty grouping instead.

For the data definitions, see figure 74.

Exercise 276. Real-World Data: iTunes explains how to analyze the information in an iTunes XML library.

Design select-album-date. The function consumes the title of an album, a date, and an LTracks. It extracts from the latter the list of tracks from the given album that have been played after the date.
Design select-albums. The function consumes an LTracks. It produces a list of LTracks, one per album. Each album is uniquely identified by its title and shows up in the result only once.

See figure 77 for the services provided by the 2htdp/itunes teachpack.

Exercise 277. Full Space War spells out a game of space war. In the basic version, a UFO descends and a player defends with a tank. One additional suggestion is to equip the UFO with charges that it can drop at the tank; the tank is destroyed if a charge comes close enough.

Inspect the code of your project for places where it can benefit from existing abstraction, that is, processing lists of shots or charges.

Once you have simplified the code with the use of existing abstractions, look for opportunities to create abstractions. Consider moving lists of objects as one example where abstraction may pay off.

Exercise 278. Feeding Worms explains how another one of the oldest computer games work. The game features a worm that moves at a constant speed in a player-controlled direction. When it encounters food, it eats the food and grows. When it runs into the wall or into itself, the game is over.

This project can also benefit from the abstract list-processing functions in ISL. Look for places to use them and replace existing code, a piece at a time. Tests will ensure that you aren’t introducing mistakes.

17 Nameless Functions🔗

Using abstract functions needs functions as arguments. Occasionally these functions are existing primitive functions, teachpack functions, or functions that you defined:

(build-list n add1) creates (list 1 ... n);
(foldr cons another-list a-list) concatenates the items in a-list and another-list into a single list; and
(foldr above empty-image images) stacks the given images.

At other times, it requires the definition of a simple helper function, a definition that often consists of a single line. Consider this use of filter:

; [List-of IR] Number -> Boolean
(define (find l th)
  (local (; IR -> Boolean
          (define (acceptable? ir)
            (<= (IR-price ir) th)))
    (filter acceptable? l)))

It finds all items on an inventory list whose price is below th. The auxiliary function is nearly trivial yet its definition takes up three lines.

This situation calls for an improvement to the language. Programmers should be able to create such small and insignificant functions without much effort.If you haven’t done so, choose “Intermediate Student with lambda” from the “How to Design Programs” submenu in the “Language” menu in DrRacket. The history of lambda is intimately involved with the early history of programming and programming language design. The next level in our hierarchy of teaching languages, “Intermediate Student Language with lambda,” solves the problem with a new concept, nameless functions. This chapter introduces the concept: its syntax, its meaning, and its pragmatics. With lambda, the above definition is, conceptually speaking, a one-liner:

; [List-of IR] Number -> Boolean
(define (find l th)
(filter (lambda (ir) (<= (IR-price ir) th)) l))

The first two sections focus the mechanics of lambda; the remaining ones use lambda for instantiating abstractions, for testing and specifying, and for representing infinite data.

17.1 Functions from lambda🔗

The syntax of lambda is straightforward:

(lambda (variable-1 ... variable-N) expression)

Its distinguishing characteristic is the keyword lambda. The keyword is followed by a sequence of variables, enclosed in a pair of parentheses. The last piece is an arbitrary expression, and it computes the result of the function when it is given values for its parameters.

Here are three simple examples, all of which consume one argument:

(lambda (x) (expt 10 x)), which assumes that the argument is a number and computes the exponent of 10 to the number;
(lambda (n) (string-append "To " n ",")), which uses a given string to synthesize an address with string-append; and
(lambda (ir) (<= (IR-price ir) th)), which is a function on an IR structure that extracts the price and compares it with th.

One way to understand how lambda works is to view it as an abbreviation for a local expression. For example,

(lambda (x) (* 10 x))

is short forThis way of thinking about lambda shows one more time why the rule for computing with local is complicated.

(local ((define (some-name x) (* 10 x)))
some-name)

This “trick” works, in general, as long as some-name does not appear in the body of the function. What this means is that lambda creates a function with a name that nobody knows. If nobody knows the name, it might as well be nameless.

To use a function created from a lambda expression, you apply it to the correct number of arguments. It works as expected:

> ((lambda (x) (expt 10 x)) 2)
100
> ((lambda (name rst) (string-append name ", " rst))
   "Robby"
   "etc.")
"Robby, etc."
> ((lambda (ir) (<= (IR-price ir) th))
   (make-IR "bear" 10))
#true

Note how the second sample function requires two arguments and that the last example assumes a definition for th in the definitions window such as this one:

(define th 20)

The result of the last example is #true because the price field of the inventory record contains 10, and 10 is less than 20.

The important point is that these nameless functions can be used wherever a function is required, including with the abstractions from figure 95:

> (map (lambda (x) (expt 10 x))
       '(1 2 3))
(list 10 100 1000)
> (foldl (lambda (name rst)
           (string-append name ", " rst))
         "etc."
         '("Matthew" "Robby"))
"Robby, Matthew, etc."
> (filter (lambda (ir) (<= (IR-price ir) th))
          (list (make-IR "bear" 10)
                (make-IR "doll" 33)))
(list (make-IR ...))

OnceThe dots are not part of the output. again, the last example assumes a definition for th.

Exercise 279. Decide which of the following phrases are legal lambda expressions:

(lambda (x y) (x y y))
(lambda () 10)
(lambda (x) x)
(lambda (x y) x)
(lambda x 10)

Explain why they are legal or illegal. If in doubt, experiment in the interactions area of DrRacket.

Exercise 280. Calculate the result of the following expressions:

((lambda (x y) (+ x (* x y)))
1 2)
((lambda (x y)
   (+ x
      (local ((define z (* y y)))
        (+ (* 3 z) (/ 1 x)))))
1 2)
((lambda (x y)
   (+ x
      ((lambda (z)
         (+ (* 3 z) (/ 1 z)))
       (* y y))))
1 2)

Check your results in DrRacket.

Exercise 281. Write down a lambda expression that

consumes a number and decides whether it is less than 10;
multiplies two given numbers and turns the result into a string;
consumes a natural number and returns 0 for evens and 1 for odds;
consumes two inventory records and compares them by price; and
adds a red dot at a given Posn to a given Image.

Demonstrate how to use these functions in the interactions area.

17.2 Computing with lambda🔗

The insight that lambda abbreviates a certain kind of local also connects constant definitions and function definitions. Instead of viewing function definitions as given, we can take lambdas as another fundamental concept and say that a function definition abbreviates a plain constant definition with a lambda expression on the right-hand side.

It’s best to look at some concrete examples:

(define (f x)
  (* 10 x))

is short for

(define f
  (lambda (x)
     (* 10 x)))

What this line says is that a function definition consists of two steps: the creation of the function and its naming. Here, the lambda on the right-hand side creates a function of one argument x that computes

; it is define that names the lambda expression f. We give names to functions for two distinct reasons. On the one hand, a function is often called more than once from other functions, and we wouldn’t want to spell out the function with a lambda each time it is called. On the other hand, functions are often recursive because they process recursive forms of data, and naming functions makes it easy to create recursive functions.

Exercise 282. Experiment with the above definitions in DrRacket.

Also add

; Number -> Boolean
(define (compare x)
(= (f-plain x) (f-lambda x)))

to the definitions area after renaming the left-hand f to f-plain and the right-hand one to f-lambda. Then run

(compare (random 100000))

a few times to make sure the two functions agree on all kinds of inputs.

If function definitions are just abbreviations for constant definitions, we can replace the function name by its lambda expression:

(f (f 42))
==
((lambda (x) (* 10 x)) ((lambda (x) (* 10 x)) 42))

Strangely though, this substitution appears to create an expression that violates the grammar as we know it. To be precise, it generates an application expression whose function position is a lambda expression.

The point is that ISL+’s grammar differs from ISL’s in two aspects: it obviously comes with lambda expressions, but it also allows arbitrary expressions to show up in the function position of an application. This means that you may need to evaluate the function position before you can proceed with an application, but you know how to evaluate most expressions. Of course, the real difference is that the evaluation of an expression may yield a lambda expression. Functions really are values. The following grammar revises the one from Intermezzo 1: Beginning Student Language to summarize these differences:

expr = ...
| (expr expr ...)

value = ...
| (lambda (variable variable ...) expr)

Alonzo Church, who invented lambda in the late 1920s, hoped to create a unifying theory of functions. He stated the beta axiom roughly like this.—From his work we know that from a theoretical perspective, a language does not need local once it has lambda. But the margin of this page is too small to explain this idea properly. If you are curious, read up on the Y combinator.

What you really need to know is how to evaluate the application of a lambda expression to arguments, and that is surprisingly straightforward:

((lambda (x-1 ... x-n) f-body) v-1 ... v-n) == f-body
; with all occurrences of x-1 ... x-n
; replaced with v-1 ... v-n, respectively [beta-v]

That is, the application of a lambda expression proceeds just like that of an ordinary function. We replace the parameters of the function with the actual argument values and compute the value of the function body.

Here is how to use this law on the first example in this chapter:

((lambda (x) (* 10 x)) 2)
==
(* 10 2)
==
20

The second one proceeds in an analogous manner:

((lambda (name rst) (string-append name ", " rst))
"Robby" "etc.")
==
(string-append "Robby" ", " "etc.")
==
"Robby, etc."

Stop! Use your intuition to calculate the third example:

((lambda (ir) (<= (IR-price ir) th))
(make-IR "bear" 10))

Assume th is larger than or equal to 10.

Exercise 283. Confirm that DrRacket’s stepper can deal with lambda. Use it to step through the third example and also to determine how DrRacket evaluates the following expressions:

(map (lambda (x) (* 10 x))
     '(1 2 3))

(foldl (lambda (name rst)
         (string-append name ", " rst))
       "etc."
       '("Matthew" "Robby"))

(filter (lambda (ir) (<= (IR-price ir) th))
        (list (make-IR "bear" 10)
              (make-IR "doll" 33)))

Exercise 284. Step through the evaluation of this expression:

((lambda (x) x) (lambda (x) x))

Now step through this one:

((lambda (x) (x x)) (lambda (x) x))

Stop! What do you think we should try next?

Yes, try to evaluate

((lambda (x) (x x)) (lambda (x) (x x)))

Be ready to hit STOP.

17.3 Abstracting with lambda🔗

Although it may take you a while to get used to lambda notation, you’ll soon notice that lambda makes short functions much more readable than local definitions. Indeed, you will find that you can adapt step 4 of the design recipe from Designing with Abstractions to use lambda instead of local. Consider the running example from that section. Its template based on local is this:

(define (dots lop)
  (local (; Posn Image -> Image
          (define (add-one-dot p scene) ...))
    (foldr add-one-dot BACKGROUND lop)))

If you spell out the parameters so that their names include signatures, you can easily pack all the information from local into a single lambda:

(define (dots lop)
(foldr (lambda (a-posn scene) ...) BACKGROUND lop))

From here, you should be able to complete the definition as well as you did from the original template:

(define (dots lop)
  (foldr (lambda (a-posn scene)
           (place-image DOT
                        (posn-x a-posn)
                        (posn-y a-posn)
                        scene))
         BACKGROUND lop))

Let’s illustrate lambda with some more examples from Using Abstractions, by Example:

the purpose of the first function is to add 3 to each x-coordinate on a given list of Posns:
; [List-of Posn] -> [List-of Posn]
(define (add-3-to-all lop)
  (map (lambda (p)
         (make-posn (+ (posn-x p) 3) (posn-y p)))
       lop))
Because map expects a function of one argument, we clearly want (lambda (p) ...). The function then deconstructs p, adds 3 to the x-coordinate, and repackages the data into a Posn.
the second one eliminates Posns whose y-coordinate is above 100:
; [List-of Posn] -> [List-of Posn]
(define (keep-good lop)
(filter (lambda (p) (<= (posn-y p) 100)) lop))
Here we know that filter needs a function of one argument that produces a Boolean. First, the lambda function extracts the y-coordinate from the Posn to which filter applies the function. Second, it checks whether it is less than or equal to 100, the desired limit.
and the third one determines whether any Posn on lop is close to some given point:
; [List-of Posn] Posn -> Boolean
(define (close? lop pt)
(ormap (lambda (p) (close-to p pt CLOSENESS))
lop))
Like the preceding two examples, ormap is a function that expects a function of one argument and applies this functional argument to every item on the given list. If any result is #true, ormap returns #true, too; if all results are #false, ormap produces #false.

It is best to compare the definitions from Using Abstractions, by Example and the definitions above side by side. When you do so, you should notice how easy the transition from local to lambda is and how concise the lambda version is in comparison to the local version. Thus, if you are ever in doubt, design with local first and then convert this tested version into one that uses lambda. Keep in mind, however, that lambda is not a cure-all. The locally defined function comes with a name that explains its purpose, and, if it is long, the use of an abstraction with a named function is much easier to understand than one with a large lambda.

The following exercises request that you solve the problems from Finger Exercises: Abstraction with lambda in ISL+ .

Exercise 285. Use map to define the function convert-euro, which converts a list of US$ amounts into a list of € amounts based on an exchange rate of US$1.06 per €.

Also use map to define convertFC, which converts a list of Fahrenheit measurements to a list of Celsius measurements.

Finally, try your hand at translate, a function that translates a list of Posns into a list of lists of pairs of numbers.

Exercise 286. An inventory record specifies the name of an inventory item, a description, the acquisition price, and the recommended sales price.

Define a function that sorts a list of inventory records by the difference between the two prices.

Exercise 287. Use filter to define eliminate-exp. The function consumes a number, ua, and a list of inventory records (containing name and price), and it produces a list of all those structures whose acquisition price is below ua.

Then use filter to define recall, which consumes the name of an inventory item, called ty, and a list of inventory records and which produces a list of inventory records that do not use the name ty.

In addition, define selection, which consumes two lists of names and selects all those from the second one that are also on the first.

Exercise 288. Use build-list and lambda to define a function that

creates the list (list 0 ... (- n 1)) for any natural number n;
creates the list (list 1 ... n) for any natural number n;
creates the list (list 1 1/2 ... 1/n) for any natural number n;
creates the list of the first n even numbers; and
creates a diagonal square of 0s and 1s; see exercise 262.

Also define tabulate with lambda.

Exercise 289. Use ormap to define find-name. The function consumes a name and a list of names. It determines whether any of the names on the latter are equal to or an extension of the former.

With andmap you can define a function that checks all names on a list of names that start with the letter "a".

Should you use ormap or andmap to define a function that ensures that no name on some list exceeds some given width?

Exercise 290. Recall that the append function in ISL concatenates the items of two lists or, equivalently, replaces '() at the end of the first list with the second list:

(equal? (append (list 1 2 3) (list 4 5 6 7 8))
(list 1 2 3 4 5 6 7 8))

Use foldr to define append-from-fold. What happens if you replace foldr with foldl?

Now use one of the fold functions to define functions that compute the sum and the product, respectively, of a list of numbers.

Exercise 291. The fold functions are so powerful that you can define almost any list-processing functions with them. Use fold to define map-via-fold, which simulates map.

17.4 Specifying with lambda🔗

Figure 99 shows a generalized sorting function that consumes a list of values and a comparison function for such values. For convenience, figure 103 reproduces the essence of the definition. The body of sort-cmp introduces two local auxiliary functions: isort and insert. In addition, the figure also comes with two test cases that illustrate the workings of sort-cmp. One demonstrates how the function works on strings and the other one on numbers.

; [X] [List-of X] [X X -> Boolean] -> [List-of X]
; sorts alon0 according to cmp

(check-expect (sort-cmp '("c" "b") string<?) '("b" "c"))
(check-expect (sort-cmp '(2 1 3 4 6 5) <) '(1 2 3 4 5 6))

(define (sort-cmp alon0 cmp)
  (local (; [List-of X] -> [List-of X]
          ; produces a variant of alon sorted by cmp
          (define (isort alon) ...)

          ; X [List-of X] -> [List-of X]
          ; inserts n into the sorted list of numbers alon
          (define (insert n alon) ...))
    (isort alon0)))
Figure 103: A general sorting function

Now take a quick look at exercise 186. It asks you to formulate check-satisfied tests for sort> using the sorted>? predicate. The former is a function that sorts lists of numbers in descending order; the latter is a function that determines whether a list of numbers is sorted in descending order. Hence, the solution of this exercise is

(check-satisfied (sort> '()) sorted>?)
(check-satisfied (sort> '(12 20 -5)) sorted>?)
(check-satisfied (sort> '(3 2 1)) sorted>?)
(check-satisfied (sort> '(1 2 3)) sorted>?)

The question is how to reformulate the tests for sort-cmp analogously.

Since sort-cmp consumes a comparison function together with a list, the generalized version of sorted>? must take one too. If so, the following test cases might look like this:

(check-satisfied (sort-cmp '("c" "b") string<?)
(sorted string<?))
(check-satisfied (sort-cmp '(2 1 3 4 6 5) <)
(sorted <))

Both (sorted string<?) and (sorted <) must produce predicates. The first one checks whether some list of strings is sorted according to string<?, and the second one whether a list of numbers is sorted via <.

We have thus worked out the desired signature and purpose of sorted:

; [X] [X X -> Boolean] -> [[List-of X] -> Boolean]
; produces a function that determines whether
; some list is sorted according to cmp
(define (sorted cmp)
...)

What we need to do now is to go through the rest of the design process.

Let’s first finish the header. Remember that the header produces a value that matches the signature and is likely to break most of the tests/examples. Here we need sorted to produce a function that consumes a list and produces a Boolean. With lambda, that’s actually straightforward:

(define (sorted cmp)
(lambda (l)
#true))

Stop! This is your first function-producing function. Read the definition again. Can you explain this definition in your own words?

Next we need examples. According to our above analysis, sorted consumes predicates such as string<? and <, but clearly, >, <=, and your own comparison functions should be acceptable, too. At first glance, this suggests test cases of the shape

(check-expect (sorted string<?) ...)
(check-expect (sorted <) ...)

But, (sorted ...) produces a function, and, according to exercise 245, it is impossible to compare functions.

Hence, to formulate reasonable test cases, we need to apply the result of (sorted ...) to appropriate lists. And, based on this insight, the test cases almost formulate themselves; indeed, they can easily be derived from those for sort-cmp in figure 103:

(check-expect [(sorted string<?) '("b" "c")] #true)
(check-expect [(sorted <) '(1 2 3 4 5 6)] #true)

Note Using square instead of parentheses highlights that the first expression produces a function, which is then applied to arguments.

From this point on, the design is quite conventional. What we basically wish to design is a generalization of sorted>? from Non-empty Lists; let’s call this function sorted/l. What is unusual about sorted/l is that it “lives” in the body of a lambda inside of sorted:

(define (sorted cmp)
  (lambda (l0)
    (local ((define (sorted/l l) ... cmp ...))
      ...)))

Even though sorted/l is defined locally, it must refer to cmp.

Exercise 292. Design the function sorted?, which comes with the following signature and purpose statement:

; [X X -> Boolean] [NEList-of X] -> Boolean
; determines whether l is sorted according to cmp

(check-expect (sorted? < '(1 2 3)) #true)
(check-expect (sorted? < '(2 1 3)) #false)

(define (sorted? cmp l)
#false)

The wish list even includes examples.

Figure 104 shows the result of the design process. The sorted function consumes a comparison function cmp and produces a predicate. The latter consumes a list l0 and uses a locally defined function to determine whether all the items in l0 are ordered via cmp. Specifically, the locally defined function checks a non-empty list; in the body of local, sorted first checks whether l0 is empty, in which case it simply produces #true because the empty list is sorted.

Stop! Could you redefine sorted to use sorted? from exercise 292? Explain why sorted/l does not consume cmp as an argument.

; [X X -> Boolean] -> [[List-of X] -> Boolean]
; is the given list l0 sorted according to cmp
(define (sorted cmp)
  (lambda (l0)
    (local (; [NEList-of X] -> Boolean
            ; is l sorted according to cmp
            (define (sorted/l l)
              (cond
                [(empty? (rest l)) #true]
                [else (and (cmp (first l) (second l))
                           (sorted/l (rest l)))])))
      (if (empty? l0) #true (sorted/l l0)))))
Figure 104: A curried predicate for checking the ordering of a list

The sorted function in figure 104 is a curried version of a function that consumes two arguments:The verb “curry” honors Haskell Curry, the second person to invent the idea. The first one was Moses Schönfinkel. cmp and l0. Instead of consuming two arguments at once, a curried function consumes one argument and then returns a function that consumes the second one.

Exercise 186 asks how to formulate a test case that exposes mistakes in sorting functions. Consider this definition:

; List-of-numbers -> List-of-numbers
; produces a sorted version of l
(define (sort-cmp/bad l)
'(9 8 7 6 5 4 3 2 1 0))

Formulating such a test case with check-expect is straightforward.

To design a predicate that exposes sort-cmp/bad as flawed, we need to understand the purpose of sort-cmp or sorting in general. It clearly is unacceptable to throw away the given list and to produce some other list in its place. That’s why the purpose statement of isort says that the function “produces a variant of” the given list. “Variant” means that the function does not throw away any of the items on the given list.

With these thoughts in mind, we can now say that we want a predicate that checks whether the result is sorted and contains all the items from the given list:

; [X] [List-of X] [X X -> Boolean] -> [[List-of X] -> Boolean]
; is l0 sorted according to cmp
; are all items in list k members of list l0
(define (sorted-variant-of k cmp)
(lambda (l0) #false))

The two lines of the purpose statement suggest examples:

(check-expect [(sorted-variant-of '(3 2) <) '(2 3)]
#true)
(check-expect [(sorted-variant-of '(3 2) <) '(3)]
#false)

Like sorted, sorted-variant-of consumes arguments and produces a function. For the first case, sorted-variant-of produces #true because the '(2 3) is sorted and it contains all numbers in '(3 2). In contrast, the function produces #false in the second case because '(3) lacks 2 from the originally given list.

A two-line purpose statement suggests two tasks, and two tasks means that the function itself is a combination of two functions:

(define (sorted-variant-of k cmp)
  (lambda (l0)
    (and (sorted? cmp l0)
         (contains? l0 k))))

The body of the function is an and expression that combines two function calls. With the call to the sorted? function from exercise 292, the function realizes the first line of the purpose statement. The second call, (contains? l0 k), is an implicit wish for an auxiliary function.

We immediately give the full definition:

; [X] [List-of X] [List-of X] -> Boolean
; are all items in list k members of list l

(check-expect (contains? '(1 2 3) '(1 4 3)) #false)
(check-expect (contains? '(1 2 3 4) '(1 3)) #true)

(define (contains? l k)
(andmap (lambda (in-k) (member? in-k l)) k))

On the one hand, we have never explained how to systematically design a function that consumes two lists, and it actually needs its own chapter; see Simultaneous Processing. On the other hand, the function definition clearly satisfies the purpose statement. The andmap expression checks that every item in k is a member? of l, which is what the purpose statement promises.

Sadly, sorted-variant-of fails to describe sorting functions properly. Consider this variant of a sorting function:

; [List-of Number] -> [List-of Number]
; produces a sorted version of l
(define (sort-cmp/worse l)
(local ((define sorted (sort-cmp l <)))
(cons (- (first sorted) 1) sorted)))

It is again easy to expose a flaw in this function with a check-expect test that it ought to pass but clearly fails:

(check-expect (sort-cmp/worse '(1 2 3)) '(1 2 3))

Surprisingly, a check-satisfied test based on sorted-variant-of succeeds:

(check-satisfied (sort-cmp/worse '(1 2 3))
(sorted-variant-of '(1 2 3) <))

Indeed, such a test succeeds for any list of numbers, not just '(1 2 3), because the predicate generator merely checks that all the items on the original list are members of the resulting list; it fails to check whether all items on the resulting list are also members of the original list.

The easiest way to add this third check to sorted-variant-of is to add a third sub-expression to the and expression:

(define (sorted-variant-of.v2 k cmp)
  (lambda (l0)
    (and (sorted? cmp l0)
         (contains? l0 k)
         (contains? k l0))))

We choose to reuse contains? but with its arguments flipped.

At this point, you may wonder why we are bothering with the development of such a predicate when we can rule out bad sorting functions with plain check-expect tests. The difference is that check-expect checks only that our sorting functions work on specific lists. With a predicate such as sorted-variant-of.v2, we can articulate the claim that a sorting function works for all possible inputs:

(define a-list (build-list-of-random-numbers 500))

(check-satisfied (sort-cmp a-list <)
(sorted-variant-of.v2 a-list <))

Let’s take a close look at these two lines. The first line generates a list of 500 numbers. Every time you ask DrRacket to evaluate this test, it is likely to generate a list never seen before. The second line is a test case that says sorting this generated list produces a list that (1) is sorted, (2) contains all the numbers on the generated list, and (3) contains nothing else. In other words, it is almost like saying that for all possible lists, sort-cmp produces outcomes that sorted-variant-of.v2 blesses.

The specification is still flawed if the given list contains duplicate elements. Construct two list of numbers—call them l1 and l2—such that (check-satisfied l1 (sorted-variant-of.v2 l2 <)) yields #true. We thank Atharva Shukla for suggesting this exercise.

Computer scientists call sorted-variant-of.v2 a specification of a sorting function. The idea that all lists of numbers pass the above test case is a theorem about the relationship between the specification of the sorting function and its implementation. If a programmer can prove this theorem with a mathematical argument, we say that the function is correct with respect to its specification. How to prove functions or programs correct is beyond the scope of this book, but a good computer science curriculum shows you in a follow-up course how to construct such proofs.

Exercise 293. Develop found?, a specification for the find function:

; [X] X [List-of X] -> [Maybe [List-of X]]
; returns the first sublist of l that starts
; with x, #false otherwise
(define (find x l)
  (cond
    [(empty? l) #false]
    [else
     (if (equal? (first l) x) l (find x (rest l)))]))

Use found? to formulate a check-satisfied test for find.

Exercise 294. Develop is-index?, a specification for index:

; [X] X [List-of X] -> [Maybe N]
; determine the index of the first occurrence
; of x in l, #false otherwise
(define (index x l)
  (cond
    [(empty? l) #false]
    [else (if (equal? (first l) x)
              0
              (local ((define i (index x (rest l))))
                (if (boolean? i) i (+ i 1))))]))

Use is-index? to formulate a check-satisfied test for index.

Exercise 295. Develop n-inside-playground?, a specification of the random-posns function below. The function generates a predicate that ensures that the length of the given list is some given count and that all Posns in this list are within a WIDTH by HEIGHT rectangle:

; distances in terms of pixels
(define WIDTH 300)
(define HEIGHT 300)

; N -> [List-of Posn]
; generates n random Posns in [0,WIDTH) by [0,HEIGHT)
(check-satisfied (random-posns 3)
                 (n-inside-playground? 3))
(define (random-posns n)
  (build-list
    n
    (lambda (i)
      (make-posn (random WIDTH) (random HEIGHT)))))

Define random-posns/bad that satisfies n-inside-playground? and does not live up to the expectations implied by the above purpose statement. Note This specification is incomplete. Although the word “partial” might come to mind, computer scientists reserve the phrase “partial specification” for a different purpose.

17.5 Representing with lambda🔗

Because functions are first-class values in ISL+, we may think of them as another form of data and use them for data representation. This section provides a taste of this idea; the next few chapters do not rely on it.

As always, we start from a representative problem:

Sample Problem Navy strategists represent fleets ofThis problem is also solvable with a self-referential data representation that says a shape is a circle, a rectangle, or a combination of two shapes. See the next part of the book for this design choice. ships as rectangles (the ships themselves) and circles (their weapons’ reach). The coverage of a fleet of ships is the combination of all these shapes. Design a data representation for rectangles, circles, and combinations of shapes. Then design a function that determines whether some point is within a shape.

The problem comes with all kinds of concrete interpretations, which we leave out here. A slightly more complex version was the subject of a programming competition in the mid-1990s run by Yale University on behalf of the US Department of Defense.

One mathematical approach considers shapes as predicates on points. That is, a shape is a function that maps a Cartesian point to a Boolean value. Let’s translate these English words into a data definition:

; A Shape is a function:
; [Posn -> Boolean]
; interpretation if s is a shape and p a Posn, (s p)
; produces #true if p is in s, #false otherwise

Its interpretation part is extensive because this data representation is so unusual. Such an unusual representation calls for an immediate exploration with examples. We delay this step for a moment, however, and instead define a function that checks whether a point is inside some shape:

; Shape Posn -> Boolean
(define (inside? s p)
(s p))

Doing so is straightforward because of the given interpretation. It also turns out that it is simpler than creating examples, and, surprisingly, the function is helpful for formulating data examples.

Stop! Explain how and why inside? works.

Now let’s return to the problem of elements of Shape. Here is a simplistic element of the class:

; Posn -> Boolean
(lambda (p) (and (= (posn-x p) 3) (= (posn-y p) 4)))

As required, it consumes a Posn p, and its body compares the coordinates of p to those of the point (3,4), meaning this function represents a single point. While the data representation of a point as a Shape might seem silly, it suggests how we can define functions that create elements of Shape: We use “mk” because this function is not an ordinary constructor.

; Number Number -> Shape
(define (mk-point x y)
(lambda (p)
(and (= (posn-x p) x) (= (posn-y p) y))))

(define a-sample-shape (mk-point 3 4))

Stop again! Convince yourself that the last line creates a data representation of (3,4). Consider using DrRacket’s stepper.

If we were to design such a function, we would formulate a purpose statement and provide some illustrative examples. For the purpose we could go with the obvious:

; creates a representation for a point at (x,y)

or, more concisely and more appropriately,

; represents a point at (x,y)

For the examples we want to go with the interpretation of Shape. To illustrate, (mk-point 3 4) is supposed to evaluate to a function that returns #true if, and only if, it is given (make-posn 3 4). Using inside?, we can express this statement via tests:

(check-expect (inside? (mk-point 3 4) (make-posn 3 4))
#true)
(check-expect (inside? (mk-point 3 4) (make-posn 3 0))
#false)

In short, to make a point representation, we define a constructor-like function that consumes the point’s two coordinates. Instead of a record, this function uses lambda to construct another function. The function that it creates consumes a Posn and determines whether its x and y fields are equal to the originally given coordinates.

Next we generalize this idea from simple points to shapes, say circles. In your geometry courses, you learn that a circle is a collection of points that all have the same distance to the center of the circle—the radius. For points inside the circle, the distance is smaller than or equal to the radius. Hence, a function that creates a Shape representation of a circle must consume three pieces: the two coordinates for its center and the radius:

; Number Number Number -> Shape
; creates a representation for a circle of radius r
; located at (center-x, center-y)
(define (mk-circle center-x center-y r)
...)

Like mk-point, it produces a function via a lambda. The function that is returned determines whether some given Posn is inside the circle. Here are some examples, again formulated as tests:

(check-expect
  (inside? (mk-circle 3 4 5) (make-posn 0 0)) #true)
(check-expect
  (inside? (mk-circle 3 4 5) (make-posn 0 9)) #false)
(check-expect
  (inside? (mk-circle 3 4 5) (make-posn -1 3)) #true)

The origin, (make-posn 0 0), is exactly five steps away from (3,4), the center of the circle; see Defining Structure Types. Stop! Explain the remaining examples.

Exercise 296. Use compass-and-pencil drawings to check the tests.

Mathematically, we say that a Posn p is inside a circle if the distance between p and the circle’s center is smaller than the radius r. Let’s wish for the right kind of helper function and write down what we have.

(define (mk-circle center-x center-y r)
  ; [Posn -> Boolean]
  (lambda (p)
    (<= (distance-between center-x center-y p) r)))

The distance-between function is a straightforward exercise.

Exercise 297. Design the function distance-between. It consumes two numbers and a Posn: x, y, and p. The function computes the distance between the points (x, y) and p.

Domain Knowledge The distance between

and

that is, the distance of

to the origin.

The data representation of a rectangle is expressed in a similar manner:

; Number Number Number Number -> Shape
; represents a width by height rectangle whose
; upper-left corner is located at (ul-x, ul-y)

(check-expect (inside? (mk-rect 0 0 10 3)
                       (make-posn 0 0))
              #true)
(check-expect (inside? (mk-rect 2 3 10 3)
                       (make-posn 4 5))
              #true)
; Stop! Formulate a negative test case.

(define (mk-rect ul-x ul-y width height)
  (lambda (p)
    (and (<= ul-x (posn-x p) (+ ul-x width))
         (<= ul-y (posn-y p) (+ ul-y height)))))

Its constructor receives four numbers: the coordinates of the upper-left corner, its width, and height. The result is again a lambda expression. As for circles, this function consumes a Posn and produces a Boolean, checking whether the x and y fields of the Posn are in the proper intervals.

At this point, we have only one task left, namely, the design of a function that maps two Shape representations to their combination. The signature and the header are easy:

; Shape Shape -> Shape
; combines two shapes into one
(define (mk-combination s1 s2)
  ; Posn -> Boolean
  (lambda (p)
    #false))

Indeed, even the default value is straightforward. We know that a shape is represented as a function from Posn to Boolean, so we write down a lambda that consumes some Posn and produces #false, meaning it says no point is in the combination.

So suppose we wish to combine the circle and the rectangle from above:

(define circle1 (mk-circle 3 4 5))
(define rectangle1 (mk-rect 0 3 10 3))
(define union1 (mk-combination circle1 rectangle1))

Some points are inside and some outside of this combination:

(check-expect (inside? union1 (make-posn 0 0)) #true)
(check-expect (inside? union1 (make-posn 0 9)) #false)
(check-expect (inside? union1 (make-posn -1 3)) #true)

Since (make-posn 0 0) is inside both, there is no question that it is inside the combination of the two. In a similar vein, (make-posn 0 9) is in neither shape, and so it isn’t in the combination. Finally, (make-posn -1 3) is in circle1 but not in rectangle1. But the point must be in the combination of the two shapes because every point that is in one or the other shape is in their combination.

This analysis of examples implies a revision of mk-combination:

; Shape Shape -> Shape
(define (mk-combination s1 s2)
  ; Posn -> Boolean
  (lambda (p)
    (or (inside? s1 p) (inside? s2 p))))

The or expression says that the result is #true if one of two expressions produces #true: (inside? s1 p) or (inside? s2 p). The first expression determines whether p is in s1 and the second one whether p is in s2. And that is precisely a translation of our above explanation into ISL+ .

Exercise 298. Design my-animate. Recall that the animate function consumes the representation of a stream of images, one per natural number. Since streams are infinitely long, ordinary compound data cannot represent them. Instead, we use functions:

; An ImageStream is a function:
; [N -> Image]
; interpretation a stream s denotes a series of images

Here is a data example:

; ImageStream
(define (create-rocket-scene height)
(place-image 50 height (empty-scene 60 60)))

You may recognize this as one of the first pieces of code in the Prologue.

The job of (my-animate s n) is to show the images (s 0), (s 1), and so on at a rate of 30 images per second up to n images total. Its result is the number of clock ticks passed since launched.

Note This case is an example where it is possible to write down examples/test cases easily, but these examples/tests per se do not inform the design process of this big-bang function. Using functions as data representations calls for more design concepts than this book supplies.

Exercise 299. Design a data representation for finite and infinite sets so that you can represent the sets of all odd numbers, all even numbers, all numbers divisible by 10, and so on.

Design the functions add-element, which adds an element to a set; union, which combines the elements of two sets; and intersect, which collects all elements common to two sets.

Hint Mathematicians deal with sets as functions that consume a potential element ed and produce #true only if ed belongs to the set.

18 Summary🔗

This third part of the book is about the role of abstraction in program design. Abstraction has two sides: creation and use. It is therefore natural if we summarize the chapter as two lessons:

Repeated code patterns call for abstraction. To abstract means to factor out the repeated pieces of code—the abstraction—and to parameterize over the differences. With the design of proper abstractions, programmers save themselves future work and headaches because mistakes, inefficiencies, and other problems are all in one place. One fix to the abstraction thus eliminates any specific problem once and for all. In contrast, the duplication of code means that a programmer must find all copies and fix all of them when a problem is found.
Most languages come with a large collection of abstractions. Some are contributions by the language design team; others are added by programmers who use the language. To enable effective reuse of these abstractions, their creators must supply the appropriate pieces of documentation—a purpose statement, a signature, and good examples—and programmers use them to apply abstractions.

All programming languages come with the means to build abstractions though some means are better than others. All programmers must get to know the means of abstraction and the abstractions that a language provides. A discerning programmer will learn to distinguish programming languages along these axes.

Beyond abstraction, this third part also introduces the idea that

functions are values, and they can represent information.

While the idea is ancient for the Lisp family of programming languages (such as ISL+) and for specialists in programming language research, it has only recently gained acceptance in most modern mainstream languages—C#, C++, Java, JavaScript, Perl, Python.

contents ← prev up next →

	Preface
	Prologue: How to Program
I	Fixed-Size Data
	Intermezzo 1: Beginning Student Language
II	Arbitrarily Large Data
	Intermezzo 2: Quote, Unquote
III	Abstraction
	Intermezzo 3: Scope and Abstraction
IV	Intertwined Data
	Intermezzo 4: The Nature of Numbers
V	Generative Recursion
	Intermezzo 5: The Cost of Computation
VI	Accumulators
	Epilogue: Moving On

14	Similarities Everywhere
15	Designing Abstractions
16	Using Abstractions
17	Nameless Functions
18	Summary

expr	=	...
	\|	(expr expr ...)

value	=	...
	\|	(lambda (variable variable ...) expr)