8.0.0.10
Prologue: How to Program
When you were a small child, your parents taught you to count
andConsider a quick look at
On Teaching Part I. perform simple calculations with your fingers:
“1 + 1 is 2”; “1 + 2 is 3”; and so on. Then they would ask “what’s 3
+ 2?” and you would count off the fingers of one hand. They programmed,
and you computed. And in some way, that’s really all there is to
programming and computing.
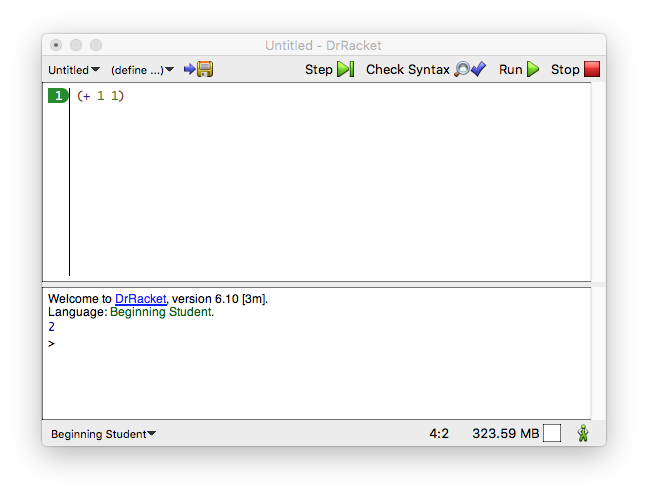
Download DrRacket from its web site.
Now it is time to switch roles. Start DrRacket. Doing so brings up the window
of
figure 3. Select “Choose language”
from the “Language” menu, which opens a dialog listing “Teaching
Languages” for “How to Design Programs.” Choose “Beginning Student”
(the Beginning Student Language, or BSL)
and click
OK to set up DrRacket. With this task
completed,
you can program, and the DrRacket software becomes the child. Start
with the simplest of all calculations. You type
into the top part of DrRacket, click RUN, and
a 2 shows up in the bottom.
Figure 3: Meet DrRacket
That’s how simple programming is. You ask questions as if DrRacket were
a child, and DrRacket computes for you. You can also ask DrRacket to process several
requests at once:
| (+ 2 2) |
| (* 3 3) |
| (- 4 2) |
| (/ 6 2) |
After you click RUN, you see
4 9 2 3
in the bottom half of DrRacket, which are the expected results.
Let’s slow down for a moment and introduce some words:
The top half of DrRacket is called the definitions area. In
this area, you create the programs, which is called editing. As
soon as you add a word or change something in the definitions area, the
SAVE button shows up in the top-left corner. When you click
SAVE for the first time, DrRacket asks you for the name of a file so
that it can store your program for good. Once your definitions area is
associated with a file, clicking SAVE ensures that the
content of the definitions area is stored safely in the file.
Programs consist of expressions. You have seen
expressions in mathematics. For now, an expression is either a plain
number or something that starts with a left parenthesis “(” and ends in
a matching right parenthesis “)”—which DrRacket rewards by shading the
area between the pair of parentheses.
When you click RUN, DrRacket evaluates the expressions in the
definitions area and shows their result in the interactions
area. Then, DrRacket, your faithful servant, awaits your commands at the
prompt (>). The appearance of the prompt signals that DrRacket is
waiting for you to enter additional expressions, which it then evaluates
like those in the definitions area:
Enter an expression at the prompt, hit the “return” or “enter” key on
your keyboard, and watch how DrRacket responds with the result. You can do
so as often as you wish:
Take a close look at the last number. Its “#i” prefix is short for “I
don’t really know the precise number so take that for now” or an
inexact number. Unlike your
calculator or other programming systems, DrRacket is
honest. When it doesn’t know the exact number, it warns you with this
special prefix. Later, we will show you really strange facts about
“computer numbers,” and you will then truly appreciate that DrRacket
issues such warnings.
By now you might be wondering whether DrRacket can add more than two
numbers at once, and yes, it can! As a matter of fact, it can do it in two
different ways:
| > (+ 2 (+ 3 4)) |
9 |
| > (+ 2 3 4) |
9 |
The first one is nested arithmetic, as you know it from school.
The second one is BSL arithmetic; and the latter is natural,
because in this notation you always use parentheses to group operations
and numbers together.
In BSL,
This book does not teach you Racket, even if the
editor is called DrRacket. See the Preface, especially the section on
DrRacket and the Teaching Languages for details on the choice to
develop our own language. every time you want to use a “calculator
operation,” you write down an opening parenthesis, the operation you wish
to perform, say
+, the numbers on which the operation should work
(separated by spaces or even line breaks), and, finally, a closing
parenthesis. The items following the operation are called the
operands. Nested arithmetic means that you can use an
expression for an operand, which is why
is a fine program. You can do this as often as you wish:
| > (+ 2 (+ (* 3 3) 4)) |
15 |
| > (+ 2 (+ (* 3 (/ 12 4)) 4)) |
15 |
| > (+ (* 5 5) (+ (* 3 (/ 12 4)) 4)) |
38 |
There are no limits to nesting, except for your patience.
Naturally, when DrRacket calculates for you, it uses the rules that you know
and love from math. Like you, it can determine the result of an addition
only when all the operands are plain numbers. If an operand is a
parenthesized operator expression—something that starts with a “(” and
an operation—it determines the result of that nested expression
first. Unlike you, it never needs to ponder which expression to
calculate first—because this first rule is the only rule there is.
The price for DrRacket’s convenience is that parentheses have meaning. You
must enter all these parentheses, and you may not enter too
many. For example, while extra parentheses are acceptable to your math
teacher, this is not the case for BSL. The expression
(+ (1) (2))
contains way too many parentheses, and DrRacket lets you know in no uncertain terms:
| > (+ (1) (2)) |
function call:expected a function after the open parenthesis, found a number |
Once you get used to BSL programming, though, you will see that it
isn’t a price at all. First, you get to use operations on several
operands at once, if it is natural to do so:
| > (+ 1 2 3 4 5 6 7 8 9 0) |
45 |
| > (* 1 2 3 4 5 6 7 8 9 0) |
0 |
If you don’t know what an operation does for several operands, enter an
example into the interactions area and hit “return”; DrRacket lets you
know whether and how it works. Or use HelpDesk to read the
documentation.As you may have noticed, the names of
operations in the on-line text are linked to the documentation in HelpDesk.
Second, when you read programs that others write, you will never have
to wonder which expressions are evaluated first. The parentheses and the
nesting will immediately tell you.
In this context, to program is to write down comprehensible arithmetic
expressions, and to compute is to determine their value. With DrRacket, it is
easy to explore this kind of programming and computing.
Arithmetic and Arithmetic
If programming were just about numbers and arithmetic, it would be as
boring as mathematics. Fortunately, there is much more to programming than
numbers: text, truths, images, and a great deal more.Just
kidding: mathematics is a fascinating subject, but you won’t need much of
it for now.
The first thing you need to know is that in BSL, text is any sequence of
keyboard characters enclosed in double quotes ("). We call it a
string. Thus, "hello world" is a perfectly fine string; and when
DrRacket evaluates this string, it just echoes it back in the interactions
area, like a number:
| > "hello world" |
"hello world" |
Indeed, many people’s first program is one that displays exactly this string.
Otherwise, you need to know that in addition to an arithmetic of numbers,
DrRacket also knows about an arithmetic of strings. So here are two
interactions that illustrate this form of arithmetic:
Just like
+,
string-append is an operation; it makes a
string by adding the second to the end of the first. As the first interaction
shows, it does this literally, without adding anything between the two
strings: no blank space, no comma, nothing. Thus, if you want to see the
phrase
"hello world", you really need to add a space to one of
these words somewhere; that’s what the second interaction shows. Of
course, the most natural way to create this phrase from the two words is
to enter
because
string-append, like
+, can handle as many
operands as desired.
You can do more with strings than append them. You can extract pieces from
a string, reverse them, render all letters uppercase (or lowercase), strip
blank spaces from the left and right, and so on. And best of all, you
don’t have to memorize any of that. If you need to know what you can do
with strings, look up the term in HelpDesk.Use F1 or the drop-down
menu on the right to open HelpDesk. Look at the manuals for BSL and its
section on pre-defined operations, especially those for strings.
If you looked up the primitive operations of BSL, you saw that
primitive (sometimes called pre-defined or
built-in) operations can consume strings and produce
numbers:
There is also an operation that converts strings into numbers:
If you expected “forty-two” or something clever along those lines,
sorry, that’s really not what you want from a string calculator.
The last expression raises a question, though. What if someone uses
string->number
with a string that is not a number wrapped within string quotes? In that
case, the operation produces a different kind of result:
This is neither a number nor a string; it is a Boolean. Unlike numbers
and strings, Boolean values come in only two varieties: #true and
#false. The first is truth, the second falsehood. Even so, DrRacket
has several operations for combining Boolean values:
| > (and #true #true) |
#true |
| > (and #true #false) |
#false |
| > (or #true #false) |
#true |
| > (or #false #false) |
#false |
| > (not #false) |
#true |
and you get the results that the name of the operation suggests. (Don’t
know what
and,
or, and
not compute? Easy:
(and x y) is true if
x and
y are true;
(or x y) is true if either
x or
y or both are
true; and
(not x) results in
#true precisely when
x is
#false.)
It is also useful to “convert” two numbers into a Boolean:
| > (> 10 9) |
#true |
| > (< -1 0) |
#true |
| > (= 42 9) |
#false |
Stop! Try the following three expressions:
(>= 10 10),
(<= -1 0), and
(string=? "design" "tinker"). This last one is different
again; but don’t worry, you can do it.
With all these new kinds of data—yes, numbers, strings, and
Boolean values are data—and operations floating around, it is easy to
forget some basics, like nested arithmetic:
What is the result of this expression? How did you figure it out? All by
yourself? Or did you just type it into DrRacket’s interactions area
and hit the “return” key? If you did the latter, do you think you would
know how to do this on your own? After all, if you can’t predict what
DrRacket does for small expressions, you may not want to trust it when
you submit larger tasks than that for evaluation.
Before we show you how to do some “real” programming, let’s discuss one
more kind of data to spice things up: images.To insert
images such as this rocket into DrRacket, use the Insert menu. Or,
copy and paste the image from your browser into DrRacket. When you
insert an image into the interactions area and hit “return” like this
> 
DrRacket replies with the image. In contrast to many other programming
languages, BSL understands images, and it supports an arithmetic of
images just as it supports an arithmetic of numbers or strings. In short,
your programs can calculate with images, and you can do so in the
interactions area. Furthermore, BSL programmers—like the programmers for
other programming languages—create libraries that others may
find helpful. Using such libraries is just like expanding your
vocabularies with new words or your programming vocabulary with new
primitives. We dub such libraries teachpacks because they are
helpful with teaching.
Add (require 2htdp/image) to the definitions
area, or select Add Teachpack from the Language menu and
choose image from the Preinstalled HtDP/2e Teachpack menu.
One important library—the 2htdp/image library—supports operations for computing
the width and height of an image:
Once you have added the library to your program, clicking RUN gives
you
1176
because that’s the area of a 28 by 42 image.
You don’t have to use Google to find images and insert them in your DrRacket
programs with the “Insert” menu. You can also instruct DrRacket to
create simple images from scratch:
When the result of an expression is an image, DrRacket draws it into the
interactions area. But otherwise, a BSL program deals with
images as data that is just like numbers. In particular, BSL has
operations for combining images in the same way that it has operations for adding
numbers or appending strings:
Overlaying these images in the opposite order produces a solid blue
square:
Stop and reflect on this last result for a moment.
As you can see,
overlay is more like
string-append than
+, but it does “add” images just like
string-append
“adds” strings and
+ adds numbers. Here is another illustration
of the idea:
These interactions with DrRacket don’t draw anything at all; they really just
measure their width.
Two more operations matter:
empty-scene and
place-image. The first creates a scene, a special kind of
rectangle. The second places an image into such a scene:
and you get this:Not quite. The image comes without a
grid. We superimpose the grid on the empty scene so that you can see where
exactly the green dot is placed.
As you can see from this image, the origin (or (0,0)) is in the upper-left
corner. Unlike in mathematics, the y-coordinate is
measured downward, not upward. Otherwise, the image shows what
you should have expected: a solid green disk at the coordinates (50,80) in
a 100 by 100 empty rectangle.
Let’s summarize again. To program is to write down an arithmetic
expression, but you’re no longer restricted to boring numbers. In BSL,
arithmetic is the arithmetic of numbers, strings, Booleans, and
even images. To compute, though, still means to determine the value of an
expression—except that this value can be a string, a number, a
Boolean, or an image.
And now you’re ready to write programs that make rockets fly.
Inputs and Output
The programs you have written so far are pretty boring. You write down an
expression or several expressions; you click RUN; you see some
results. If you click RUN again, you see the exact same results. As
a matter of fact, you can click RUN as often as you want, and the
same results show up. In short, your programs really are like calculations
on a pocket calculator, except that DrRacket calculates with all kinds
of data, not just numbers.
That’s good news and bad news. It is good because programming and computing
ought to be a natural generalization of using a calculator. It is bad
because the purpose of programming is to deal with lots of data and to get
lots of different results, with more or less the same calculations. (It
should also compute these results quickly, at least faster than we can.)
That is, you need to learn more still before you know how to program. No
need to worry though: with all your knowledge about arithmetic of numbers,
strings, Boolean values, and images, you’re almost ready to write a program
that creates movies, not just some silly program for displaying “hello
world” somewhere. And that’s what we’re going to do next.
Just in case you didn’t know, a movie is a sequence of images that are
rapidly displayed in order. If your algebra teachers had known about the
“arithmetic of images” that you saw in the preceding section, you could
have produced movies in algebra instead of boring number
sequences. Well, here is one more such table:
x = | | 1 | | 2 | | 3 | | 4 | | 5 | | 6 | | 7 | | 8 | | 9 | | 10 |
|
y = | | 1 | | 4 | | 9 | | 16 | | 25 | | 36 | | 49 | | 64 | | 81 | | ? |
Your teachers would now ask you to fill in the blank, that is, replace the “?”
mark with a number.
It turns out that making a movie is no more complicated than completing a
table of numbers like that. Indeed, it is all about such tables:
To be concrete, your teacher should ask you here to draw the fourth image,
the fifth, and the 1273rd one because a movie is just a lot of
images, some 20 or 30 of them per second. So you need some 1200 to 1800
of them to make one minute’s worth of it.
You may also recall that your teacher not only asked for the fourth or
fifth number in some sequence but also for an expression that
determines any element of the sequence from a given x. In the
numeric example, the teacher wants to see something like
this:
If you plug in 1, 2, 3, and so on for x, you get 1, 4, 9, and so on for
y—just as the table says. For the sequence of images, you could say
something like
y = the image that contains a dot x2 pixels below the top.
The key is that these one-liners are not just expressions but functions.
At first glance, functions are like expressions, always with a
y on the
left, followed by an
= sign, and an expression. They aren’t expressions,
however. And the notation you often see in school for functions is
utterly misleading. In DrRacket, you therefore write functions a bit
differently:
The
define says “consider
y a function,” which, like
an expression, computes a value. A function’s value, though, depends on
the value of something called the
input, which we express with
(y x). Since we
don’t know what this input is, we use a name to represent the
input. Following the mathematical tradition, we use
x here
to stand in for the unknown input; but pretty soon, we will use all kinds
of names.
This second part means you must supply one number—for x—to
determine a specific value for y. When you do, DrRacket plugs the
value for x into the expression associated with the
function. Here the expression is (* x x). Once x is
replaced with a value, say 1, DrRacket can compute the result of the
expressions, which is also called the output of the function.
Click RUN and watch nothing happen. Nothing shows up in the
interactions area. Nothing seems to change anywhere else in
DrRacket. It is as if you hadn’t accomplished anything. But you
did. You actually defined a function and informed DrRacket about its
existence. As a matter of fact, the latter is now ready for you to use the
function. Enter
at the prompt in the interactions area and watch a 1 appear in
response. The (y 1) is called a function application in
DrRacket.Mathematics also calls y(1) a function
application, but your teachers forgot to tell you. Try
and see a 4 pop out. Of course, you can also enter all these
expressions in the definitions area and click RUN:
| (define (y x) (* x x)) |
| |
| (y 1) |
| (y 2) |
| (y 3) |
| (y 4) |
| (y 5) |
In response, DrRacket displays:
1 4 9 16 25,
which are the numbers from the table. Now determine the missing entry.
What all this means for you is that functions provide a rather economic way
of computing lots of interesting values with a single expression. Indeed,
programs are functions; and once you understand functions well, you know
almost everything there is to know about programming. Given their importance,
let’s recap what we know about functions so far:
First,
(define (FunctionName InputName) BodyExpression)
is a
function definition. You recognize it as such because it
starts with the “
define” keyword. It essentially
consists of three pieces: two names and an expression. The first name is
the name of the function; you need it to apply the function as often as
you wish. The second name—
called a
parameter—
represents the input of the function, which is
unknown until you apply the function. The expression, dubbed
body, computes the output of the function for a specific
input.
Second,
(FunctionName ArgumentExpression)
is a function application. The first part tells DrRacket which
function you wish to use. The second part is the input to which you want
to apply the function. If you were reading a Windows or a Mac manual, it
might tell you that this expression “launches” the
“application” called FunctionName and that it is going to
process ArgumentExpression as the input. Like all expressions,
the latter is possibly a plain piece of data or a deeply nested expression.
Functions can input more than numbers, and they can output all kinds of
data, too. Our next task is to create a function that simulates the
second table—
the one with images of a colored dot—
just like the first
function simulated the numeric table. Since the creation of images from
expressions isn’t something you know from high school, let’s start
simply. Do you remember
empty-scene? We quickly mentioned it at
the end of the previous section. When you type it into the interactions
area, like that:
DrRacket produces an empty rectangle, also called a scene.
You can add images to a scene with
place-image:
Think of the rocket as an object that is like the dot in the above table
from your mathematics class. The difference is that a rocket is interesting.
Next, you should make the rocket descend, just like the dot in the above
table. From the preceding section, you know how to achieve this effect by
increasing the y-coordinate that is supplied to
place-image:
All that’s needed now is to produce lots of these scenes easily and to
display all of them in rapid order.
Figure 4: Landing a rocket (version 1)
The first goal can be achieved with a function, of course; see
figure 4.
In BSL, you can use all kinds of characters in
names, including “-” and “.”. Yes, this is a function
definition. Instead of
y, it uses the name
picture-of-rocket, a name that immediately tells you what the
function outputs: a scene with a rocket. Instead of
x, the
function definition uses
height for the name of its parameter, a
name that suggests that it is a number and that it tells the function
where to place the rocket. The body expression of the function is exactly
like the series of expressions with which we just experimented, except
that it uses
height in place of a number. And we can easily
create all of those images with this one function:
| (picture-of-rocket 0) |
| (picture-of-rocket 10) |
| (picture-of-rocket 20) |
| (picture-of-rocket 30) |
Try this out in the definitions area or the interactions
area; both create the expected scenes.
The second goal requires knowledge about one additional primitive
operation from
the 2htdp/universe library:
animate.
Don’t forget to add the 2htdp/universe library to your
definitions area. So, click
RUN and
enter the following expression:
Stop and note that the argument expression is a function. Don’t
worry for now about using functions as arguments; it works well with
animate, but don’t try to define functions like
animate
at home just yet.
As soon as you hit the “return” key, DrRacket evaluates the expression; but
it does not display a result, not even a prompt. It opens
another window—a canvas—and starts a clock that ticks 28
times per second. Every time the clock ticks, DrRacket applies
picture-of-rocket to the number of ticks passed since this
function call. The results of these function calls are displayed in the
canvas, and it produces the effect of an animated movie. The simulation
runs until you close the window. At that point,
animate returns the number of ticks that have passed.
The question is where the images on the window come from. The short
explanation is that
animate runs its operand on the numbers
0,
1,
2, and so on,
Exercise 298
explains how to design animate. and displays the resulting
images. The long explanation is this:
animate starts a clock and counts the number of ticks;
the clock ticks 28 times per second;
every time the clock ticks, animate applies the function
picture-of-rocket to the current clock tick; and
the scene that this application creates is displayed on the canvas.
This means that the rocket first appears at height 0, then
1, then 2, and so on, which explains why the rocket descends
from the top of the canvas to the bottom. That is, our three-line program
creates some 100 pictures in about 3.5 seconds, and displaying these
pictures rapidly creates the effect of a rocket descending to the ground.
So here is what you learned in this section. Functions are useful because they
can process lots of data in a short time. You can launch a function by
hand on a few select inputs to ensure that it produces the proper outputs. This
is called testing a function. Or, DrRacket can launch a function on lots of
inputs with the help of some libraries; when you do that, you are running
the function. Naturally, DrRacket can launch functions when you press a key
on your keyboard or when you manipulate the mouse of your computer. To
find out how, keep reading. Whatever triggers a function application isn’t
important, but do keep in mind that (simple) programs are functions.
Many Ways to Compute
When you evaluate (animate picture-of-rocket), the rocket
eventually disappears into the ground. As Venkat
Pamulapati notes, SpaceX has landed many rockets vertically since
these words were written. That’s plain silly. Rockets in old
science fiction movies don’t sink into the ground; they gracefully land on
their bottoms, and the movie should end right there.
This idea suggests that computations should proceed differently, depending
on the situation. In our example, the picture-of-rocket program
should work “as is” while the rocket is in flight. When the rocket’s
bottom touches the bottom of the canvas, however, it should stop the
rocket from descending any farther.
In a sense, the idea shouldn’t be new to you. Even your mathematics
teachers define functions that distinguish various situations:
This sign function distinguishes three kinds of inputs: those
numbers that are larger than 0, those equal to 0, and those
smaller than 0. Depending on the input, the result of the
function is +1, 0, or -1.
You can define this function in DrRacket without much ado using a
conditional expression:
After you click RUN, you can interact with sign like any
other function:Open a new tab in DrRacket and start with a clean slate.
| > (sign 10) |
1 |
| > (sign -5) |
-1 |
| > (sign 0) |
0 |
This is a good time to explore what the STEP button
does. Add (sign -5) to the definitions area and click
STEP for the above sign program. When the new window
comes up, click the right and left arrows there.
In general, a conditional expression has the shape
| (cond |
| [ConditionExpression1 ResultExpression1] |
| [ConditionExpression2 ResultExpression2] |
| ... |
| [ConditionExpressionN ResultExpressionN]) |
That is, a
conditional expression consists of as many
conditional lines as needed. Each line contains two expressions:
the left one is often called
condition, and the right one is
called
result; occasionally we also use
question and
answer. To evaluate a
cond expression, DrRacket evaluates
the first condition expression,
ConditionExpression1. If this
yields
#true, DrRacket replaces the
cond expression with
ResultExpression1, evaluates it, and uses the value as the
result of the entire
cond expression. If the evaluation of
ConditionExpression1 yields
#false, DrRacket drops the
first line and starts over. In case all condition expressions evaluate to
#false, DrRacket signals an error.
Figure 5: Landing a rocket (version 2)
With this knowledge, you can now change the course of the simulation. The
goal is to not let the rocket descend below the ground level of a
100-by-60 scene. Since the picture-of-rocket function consumes
the height where it should place the rocket in the scene, a simple test
comparing the given height to the maximum height appears to suffice.
See figure 5 for the revised function definition. The
definition uses the name picture-of-rocket.v2 to distinguish
the two versions. Using distinct names also allows us to use both
functions in the interactions area and to compare the results. Here is how
the original version works:
| > (picture-of-rocket 5555) |
|
And here is the second one:
| > (picture-of-rocket.v2 5555) |
|
No matter what number you give to picture-of-rocket.v2, if it
is over 60, you get the same scene. In particular, when you run
the rocket descends and sinks halfway into the ground before it stops.
Stop! What do you think we want to see?
Landing the rocket this far down is ugly. Then again, you know how to fix
this aspect of the program. As you have seen, BSL knows an arithmetic
of images. When place-image adds an image to a scene, it uses its
center point as if it were the whole image, even though the image has a
real height and a real width. As you may recall, you can measure the
height of an image with the operation image-height. This function
comes in handy here because you really want to fly the rocket only until
its bottom touches the ground.
Putting one and one together you can now figure out that
is the point at which you want the rocket to stop its descent. You
could figure this out by playing with the program directly, or you can
experiment in the interactions area with your image arithmetic.
Here is a first attempt:
Now replace the third argument in the above application with
Stop! Conduct the experiments. Which result do you like better?
Figure 6: Landing a rocket (version 3)
When you think and experiment along these lines, you eventually get to the
program in figure 6.
Given some number, which represents the height of the rocket, it
first tests whether the rocket’s bottom is above the ground. If it is, it
places the rocket into the scene as before. If it isn’t, it places the
rocket’s image so that its bottom touches the ground.
One Program, Many Definitions
Now suppose your friends watch the animation but don’t like the size of
your canvas. They might request a version that uses
200-by-400 scenes. This simple request forces you to
replace 100 with 400 in five places in the program and
60 with 200 in two other places—not to speak
of the occurrences of 50, which really means “middle of the
canvas.”
Stop! Before you read on, try to do just that so that you get an idea of
how difficult it is to execute this request for a five-line program. As
you read on, keep in mind that programs in the world consist of 50,000 or 500,000
or even 5,000,000 or more lines of program code.
In the ideal program, a small request, such as changing the sizes of the
canvas, should require an equally small change. The tool to achieve this
simplicity with BSL is
define. In addition to defining functions,
you can also introduce
constant definitions, which assign some
name to a constant. The general shape of a constant definition is
straightforward:
Thus, for example, if you write down
in your program, you are saying that
HEIGHT always
represents the number
60. The meaning of such a definition is
what you expect. Whenever DrRacket encounters
HEIGHT during its
calculations, it uses
60 instead.
Figure 7: Landing a rocket (version 4)
Now take a look at the code in
figure 7, which implements this
simple change and also names the image of the rocket. Copy the program
into DrRacket; and after clicking
RUN, evaluate the following
interaction:
Confirm that the program still functions as before.
The program in figure 7 consists of four definitions: one
function definition and three constant definitions. The numbers
100 and 60 occur only twice—once as the value of
WIDTH and once as the value of HEIGHT. You may also
have noticed that it uses h instead of height for the
function parameter of picture-of-rocket.v4. Strictly speaking,
this change isn’t necessary because DrRacket doesn’t confuse height
with HEIGHT, but we did it to avoid confusing you.
When DrRacket evaluates (animate picture-of-rocket.v4), it replaces
HEIGHT with 60, WIDTH with 100, and
ROCKET with the image every time it encounters these names. To
experience the joys of real programmers, change the 60 next to
HEIGHT into a 400 and click RUN. You see a
rocket descending and landing in a 100 by 400 scene. One small change did
it all.
In modern parlance, you have just experienced your first program
refactoring. Every time you reorganize your program to prepare yourself
for likely future change requests, you refactor your program. Put it on
your resume. It sounds good, and your future employer probably enjoys
reading such buzzwords, even if it doesn’t make you a good programmer.
What a good programmer would never live with, however, is having a program
contain the same expression three times:
Every time your friends and colleagues read this program, they need to
understand what this expression computes, namely, the distance between the
top of the canvas and the center point of a rocket resting on the
ground. Every time DrRacket computes the value of the expressions, it
has to perform three steps: (1) determine the height of the
image; (2) divide it by 2; and (3) subtract the result from
HEIGHT. And, every time, it comes up with the same number.
This observation calls for the introduction of one more definition:
Now substitute
ROCKET-CENTER-TO-TOP for the expression
(- HEIGHT (/ (image-height ROCKET) 2)) in the rest of
the program. You may be wondering whether
this definition should be placed above or below the definition for
HEIGHT. More generally, you should be wondering whether the
ordering of definitions matters. The answer is that for constant
definitions, the order matters; and for function definitions, it
doesn’t. As soon as DrRacket encounters a constant definition, it determines
the value of the expression and then associates the name with this
value. For example,
causes DrRacket to complain that “CENTER is used before
its definition,” when it encounters the definition for
HEIGHT. In contrast,
works as expected. First, DrRacket associates
CENTER with
100. Second, it evaluates
(* 2 CENTER), which yields
200. Finally, DrRacket associates
200 with
HEIGHT.
While the order of constant definitions matters, it does not matter where
you place constant definitions relative to function definitions. Indeed,
if your program consists of many function definitions, their order doesn’t
matter either, though it is good to introduce all constant definitions
first, followed by the definitions of functions in decreasing order of
importance. When you start writing your own multi-definition programs, you
will see why this ordering matters.
Figure 8: Landing a rocket (version 5)
The program also contains two line comments,
introduced with semicolons (“;”). While DrRacket ignores such comments,
people who read programs should not because comments are intended for
human readers. It is a “back channel” of communication between the
author of the program and all of its future readers to convey information
about the program.
Once you eliminate all repeated expressions, you get the program in
figure 8. It consists of one function definition and five
constant definitions. Beyond the placement of the rocket’s center, these
constant definitions also factor out the image itself as well as the
creation of the empty scene.
Before you read on, ponder the following changes to your program:
How would you change the program to create a
200-by-400 scene?
How would you change the program so that it depicts the landing of a
green UFO (unidentified flying object)? Drawing the UFO is easy:
How would you change the program so that the background is always
blue?
How would you change the program so that the rocket lands on a flat rock
bed that is 10 pixels higher than the bottom of the scene? Don’t forget to
change the scenery, too.
Better than pondering is doing. It’s the only way to learn. So don’t let
us stop you. Just do it.
Magic Numbers Take another look at
picture-of-rocket.v5. Because we eliminated all repeated
expressions, all but one number disappeared from this function
definition. In the world of programming, these numbers are called
magic numbers, and nobody likes them. Before you know it, you
forget what role the number plays and what changes are legitimate. It is
best to name such numbers in a definition.
Here we actually know that 50 is our choice for an
x-coordinate for the rocket. Even though 50 doesn’t look
like much of an expression, it really is a repeated expression, too.
Thus, we have two reasons to eliminate 50 from the
function definition, and we leave it to you to do so.
One More Definition
Recall that
animate actually applies its functions to the number
of clock ticks that have passed since it was first called. That is, the
argument to
picture-of-rocket isn’t a height but a time. Our
previous definitions of
picture-of-rocket use the wrong name
for
Danger ahead! This section introduces one piece of
knowledge from physics. If physics scares you, skip it on a first reading;
programming doesn’t require physics knowledge. the argument of the
function; instead of
h—
short for height—
it ought to use
t for time:
| (define (picture-of-rocket t) |
| (cond |
| [(<= t ROCKET-CENTER-TO-TOP) |
| (place-image ROCKET 50 t MTSCN)] |
| [(> t ROCKET-CENTER-TO-TOP) |
| (place-image ROCKET |
| 50 ROCKET-CENTER-TO-TOP |
| MTSCN)])) |
And this small change to the definition immediately clarifies that
this program uses time as if it were a distance. What a bad idea.
Even if you have never taken a physics course, you know that a time is not
a distance. So somehow our program worked by accident. Don’t worry,
though; it is all easy to fix. All you need to know is a bit of rocket
science, which people like us call physics.
Physics?!? Well, perhaps you have already forgotten what you learned in
that course. Or perhaps you have never taken a course on physics because
you are way too young or gentle. No worries. This happens to the best
programmers all the time because they need to help people with problems in
music, economics, photography, nursing, and all kinds of other
disciplines. Obviously, not even programmers know everything. So they
look up what they need to know. Or they talk to the right kind of
people. And if you talk to a physicist, you will find out that the
distance traveled is proportional to the time:
That is, if the velocity of an object is v, then the object travels
d miles (or meters or pixels or whatever) in t seconds.
Of course, a teacher ought to show you a proper function definition:
because this tells everyone immediately that the computation of
d
depends on
t and that
v is a constant. A programmer goes
even further and uses meaningful names for these one-letter abbreviations:
This program fragment consists of two definitions: a function
distance that computes the distance traveled by an object
traveling at a constant velocity, and a constant V that describes the
velocity.
You might wonder why V is 3 here. There is no special
reason. We consider 3 pixels per clock tick a good velocity. You
may not. Play with this number and see what happens with the animation.
Figure 9: Landing a rocket (version 6)
Now we can fix
picture-of-rocket again. Instead of comparing
t with a height, the function can use
(distance t) to
calculate how far down the rocket is. The final program is displayed in
figure 9. It consists of two function definitions:
picture-of-rocket.v6 and
distance. The remaining
constant definitions make the function definitions readable and
modifiable. As always, you can run this program with
animate:
In comparison to the previous versions of picture-of-rocket,
this one shows that a program may consist of several function definitions
that refer to each other. Then again, even the first version used
+ and /—it’s just that you think of those as built
into BSL.
As you become a true-blue programmer, you will find out that programs
consist of many function definitions and many constant definitions. You
will also see that functions refer to each other all the time. What you
really need to practice is to organize them so that you can read them
easily, even months after completion. After all, an older version of
you—or someone else—will want to make changes to these programs; and
if you cannot understand the program’s organization,
you will have a difficult time with even the smallest task. Otherwise, you
mostly know what there is to know.
You Are a Programmer Now
The claim that you are a programmer may have come as a surprise to you at
the end of the preceding section, but it is true. You know all the
mechanics that there are to know about BSL. You know that programming uses
the arithmetic of numbers, strings, images, and whatever other data
your chosen programming languages support. You know that programs consist
of function and constant definitions. You know, because we have told you,
that in the end, it’s all about organizing these definitions
properly. Last but not least, you know that DrRacket and the teachpacks
support lots of other functions and that DrRacket’s HelpDesk explains what these
functions do.
You might think that you still don’t know enough to write programs that
react to keystrokes, mouse clicks, and so on. As it turns out, you do. In
addition to the animate function, the 2htdp/universe library
provides other functions that hook up your programs to the keyboard, the
mouse, the clock, and other moving parts in your computer. Indeed, it even
supports writing programs that connect your computer with anybody else’s
computer around the world. So this isn’t really a problem.
In short, you have seen almost all the mechanics of putting together
programs. If you read up on all the functions that are available, you can
write programs that play interesting computer games, run simulations, or
keep track of business accounts. The question is whether this really means
you are a programmer. Are you?
Stop! Don’t turn the page yet. Think!
Not!
When you look at the “programming” bookshelves in a random bookstore,
you will see loads of books that promise to turn you into a programmer on
the spot. Now that you have worked your way through some first examples,
however, you probably realize that this cannot possibly happen.
Acquiring the mechanical skills of programming—learning to write
expressions that the computer understands, getting to know which functions
and libraries are available, and similar activities—isn’t helping you
all that much with real programming. If it were, you could equally
well learn a foreign language by memorizing a thousand words from the
dictionary and a few rules from a grammar book.
Good programming is far more than the mechanics of acquiring a
language. Most importantly, it is about keeping in mind that programmers
create programs for other people to read them in the future. A good
program reflects the problem statements and its important concepts. It
comes with a concise self-description. Examples illustrate this
description and relate it back to the problem. The examples make sure that
the future reader knows why and how your code works. In short, good
programming is about solving problems systematically and conveying the
system within the code. Best of all, this approach to programming actually
makes programming accessible to everyone—so it serves two masters at
once.
The rest of this book is all about these things; very little of the book’s
content is actually about the mechanics of DrRacket, BSL, or
libraries. The book shows you how good programmers think about problems.
And, you will even learn that this way of solving problems applies to
other situations in life, such as the work of doctors, journalists, lawyers,
and engineers.
Oh, and by the way, the rest of the book uses a tone that is more
appropriate for a serious text than this Prologue. Enjoy!
Note on What This Book Is Not About Introductory books on
programming tend to contain lots of material about the authors’ favorite application
discipline: puzzles, mathematics, physics, music, and so on. Such material
is natural because programming is obviously useful in all these areas, but
it also distracts from the essential elements of programming. Hence, we
have made every attempt to minimize the use of knowledge from other areas
so that we can focus on what computer science can teach you about
computational problem solving.
50 23 (empty-scene 100 60))
50 20 (empty-scene 100 60))
50 30 (empty-scene 100 60))
50 40 (empty-scene 100 60))
