7.2.0.5
Intermezzo 2: Quote, Unquote
Lists play an important role in our book as well as in Racket,
the basis of our teaching languages.Be sure to set your
language level to BSL+ or up. For the design of programs, it is
critical to understand how lists are constructed from first principles; it
informs the creation of our programs. Routine work with lists calls for a
compact notation, however, like the list function introduced in
The list Function.
Since the late 1950s, Lisp-style languages have come with an even more
powerful pair of list-creation tools: quotation and anti-quotation. Many
programming languages support them now, and the PHP web page design
language injected the idea into the commercial world.
This intermezzo gives you a taste of this quotation mechanism. It also
introduces symbols, a form of data that is intimately tied to
quotation. While this introduction is informal and uses simplistic
examples, the rest of the book illustrates the power of the idea
with near-realistic variants. Come back to this intermezzo if any
of these examples cause you trouble.
Quote
Quotation is a short-hand mechanism for writing down a large list
easily. Roughly speaking, a list constructed with the list
function can be constructed even more concisely by quoting
lists. Conversely, a quoted list abbreviates a construction with
list.
Technically,
quote is a keyword for a compound sentence in the
spirit of
Intermezzo 1: Beginning Student Language and it is used like this:
(quote (1 2 3)).
DrRacket translates this expression to
(list 1 2 3). At this point,
you may wonder why we call
quote an abbreviation because the
quoted expression looks more complicated than its
translation. The key is that
' is a short-hand for
quote. Here
are some short examples, then:
| > '(1 2 3) |
(list 1 2 3) |
| > '("a" "b" "c") |
(list "a" "b" "c") |
| > '(#true "hello world" 42) |
(list #true "hello world" 42) |
As you can see, the use of
' creates the promised lists.
In case you forgot what
(list 1 2 3) means, reread
The list Function; it explains that this list is short for
(cons 1 (cons 2 (cons 3 '()))).
So far
quote looks like a small improvement over
list,
but look:
| > '(("a" 1) | | ("b" 2) | | ("d" 4)) |
|
(list (list "a" 1) (list "b" 2) (list "d" 4)) |
With ' we can construct lists as well as nested lists.
To understand how
quote works, imagine it as a function that traverses
the shape it is given. When
' encounters a plain piece of data—
a number, a
string, a Boolean, or an image—
it disappears. When it sits in front of an
open parenthesis,
(, it inserts
list to the right of the
parenthesis and puts
' on all the items between
( and the closing
). For example,
| '(1 2 3) | | is short for | | (list '1 '2 '3) |
As you already know, ' disappears from numbers so the rest is easy. Here
is an example that creates nested lists:
| '(("a" 1) 3) | | is short for | | (list '("a" 1) '3) |
To continue this example, we expand the abbreviation in the first position:
We leave it to you to wrap up this example.
Exercise 231. Eliminate
quote in favor of
list from these
expressions:
Now eliminate
list in favor of
cons where needed.
Quasiquote and Unquote
The preceding section should convince you of the advantages of ' and
quote. You may even wonder why the book introduces quote
only now and didn’t do so right from the start. It seems to greatly facilitate the
formulation of test cases that involve lists as well as for keeping track
of large collections of data. But all good things come with surprises, and
that includes quote.
When it comes to program design, it is misleading for beginners to think of lists
as quoted or even list-constructed values. The construction of
lists with cons is far more illuminating for the step-wise creation of
programs than short-hands such as quote, which hide the underlying
construction. So don’t forget to think of cons whenever you are
stuck during the design of a list-processing function.
Let’s move on, then, to the actual surprises hidden behind
quote. Suppose
your definitions area contains one constant definition:
Imagine running this program and experimenting with
in the interactions area. What result do you expect? Stop! Try to apply the
above rules of ' for a moment.
Here is the experiment
| > '(40 41 x 43 44) |
(list 40 41 'x 43 44) |
At this point it is important to remember that DrRacket displays
values. Everything on the list is a value, including
'x. It is a
value you have never seen before, namely, a
Symbol. For our
purposes, a symbol looks like a variable name except that it starts with
' and that
a symbol is a value. Variables only stand for values;
they are not values in and of themselves. Symbols play a role similar to
those of strings; they are a great way to represent symbolic information
as data.
Intertwined Data illustrates how; for now, we just accept
symbols as yet another form of data.
To drive home the idea of symbols, consider a second example:
You might expect that this expression constructs
(list 1 2 3). If
you use the rules for expanding
', however, you discover that
| '(1 (+ 1 1) 3) | | is short for | | (list '1 '(+ 1 1) '3) |
And the ' on the second item in this list does not disappear. Instead, it
abbreviates the construction of another list so that the entire example comes
out as
What this means is that
'+ is a symbol just like
'x. Just
as the latter is unrelated to the variable
x, the former has no
immediate relationship to the function
+ that comes with BSL+.
Then again, you should be able to imagine that
'+ could serve as an
elegant
data representation of the function
+ just as
'(+ 1 1)
could serve as a data representation of
(+ 1 1).
Intertwined Data picks up this idea.
In some cases, you do not want to create a nested list. You actually want
a true expression in a quoted list and you want to evaluate the
expression during the construction of the list. For such cases, you want
to use quasiquote, which, like quote, is just a
keyword for a compound sentence: (quasiquote (1 2 3)). And, like
quote, quasiquote comes with a short-hand, namely the
` character, which is the “other” single-quote key on your keyboard.
At first glance, ` acts just like ' in that it constructs lists:
| > `(1 2 3) |
(list 1 2 3) |
| > `("a" "b" "c") |
(list "a" "b" "c") |
| > `(#true "hello world" 42) |
(list #true "hello world" 42) |
The best part about
` is that you can also use it to
unquote, that is,
you can demand an escape back to the programming language proper inside
of a
quasiquoted list. Let’s illustrate the idea with the above
examples:
| > `(40 41 ,x 43 44) |
(list 40 41 42 43 44) |
| > `(1 ,(+ 1 1) 3) |
(list 1 2 3) |
As above, the first interaction assumes a definitions area that contains
(define x 42). The best way to understand this syntax is to see
it with actual keywords instead of
` and
, short-hands:
The rules for expanding a
quasiquoted and an
unquoted
shape are those of
quote supplemented with one rule. When
`
appears in front of a parenthesis, it is distributed over all parts
between it and the matching closing parenthesis. When it appears next to a
basic piece of data, it disappears. When it is in front of some variable
name, you get a symbol. And the new rule is that when
` is immediately
followed by
unquote, both characters disappear:
| `(1 ,(+ 1 1) 3) | | is short for | | (list `1 `,(+ 1 1) `3) |
and
| (list `1 `,(+ 1 1) `3) | | is short for | | (list 1 (+ 1 1) 3) |
And this is how you get
(list 1 2 3) as seen above.
From here it is a short step to the production of web pages. Yes, you read
correctly—web pages! In principle, web pages are coded in the HTML and
CSS programming languages. But nobody writes down HTML programs directly;
instead people design programs that produce web pages. Not surprisingly,
you can write such functions in BSL+, too, and there is a simplistic
example in figure 83.
As you can immediately see, this function consumes two strings and
produces a deeply nested list—a data representation of a web page.
| ; String String -> ... deeply nested list ... |
| ; produces a web page with given author and title |
| (define (my-first-web-page author title) |
| `(html |
| (head |
| (title ,title) |
| (meta ((http-equiv "content-type") |
| (content "text-html")))) |
| (body |
| (h1 ,title) |
| (p "I, " ,author ", made this page.")))) |
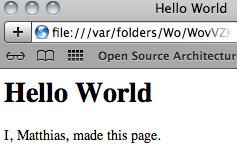
Figure 83: A simplistic HTML generator
A second look also shows that the title parameter shows up twice
in the function body: once nested in a nested list labeled with
'head and once nested in the nested list labeled with
'body. The other parameter shows up only once. We consider the
nested list a page template, and the parameters are holes in the template,
to be filled by useful values. As you can imagine, this template-driven
style of creating web pages is most
useful when you wish to create many similar pages for a site.
Nested List Representation | | Web Page Code (HTML) |
| '(html | | (head | | (title "Hello World") | | | | | | (meta | | ((http-equiv "content-type") | | (content "text-html")))) | | | | (body | | (h1 "Hello World") | | | | | | (p "I, " | | "Matthias" | | ", made this page."))) |
| | <html> | <head> | <title> | Hello World | </title> | <meta | http-equiv="content-type" | content="text-html" /> | </head> | <body> | <h1> | Hello World | </h1> | <p> | I, | Matthias, | made this page. | </p> | </body> | </html> |
|
Figure 84: A data representation based on nested lists
To understand how the function works, we experiment in DrRacket’s interactions
area. Given your knowledge of
quasiquote and
unquote,
you should be able to predict what the result of
(my-first-web-page "Matthias" "Hello World")
is. Then again, DrRacket is so fast that it is better to show you the result:
see the left column in
figure 84.
You
can use show-in-browser from the web-io.rkt library to display the
result in a web browser. The right column of the table contains the
equivalent code in HTML. If you
were to open this web page in a browser you would see something like this:
Note that "Hello World" shows up twice again: once in the title
bar of the web browser—which is due to the <title>
specification—and once in the text of the web page.
If this were 1993, you could now sell the above function as a Dot Com
company that generates people’s first web page with a simple function
call. Alas, in this day and age, it is only an exercise.
Exercise 232. Eliminate
quasiquote and
unquote from
the following expressions so that they are written with
list instead:
Also write down the nested lists that the expressions produce.
Unquote Splice
When
quasiquote meets
unquote during the expansion of
short-hands, the two annihilate each other:
| `(tr | | ,(make-row | | '(3 4 5))) |
| | is short for | | |
Thus, whatever make-row produces becomes the second item of the
list. In particular, if make-row produces a list, this list becomes the
second item of a list. If make-row translates the given list of
numbers into a list of strings, then the result is
In some cases, however, we may want to splice such a nested list into the outer
one, so that for our running example we would get
One way to solve this small problem is to fall back on
cons. That is, to
mix
cons with
quote,
quasiquote, and
unquote. After all, all of these characters are just short-hands for
consed lists. Here is what is needed to get the desired result in our
example:
(cons 'tr (make-row '(3 4 5)))
Convince yourself that the result is
(list 'tr "3" "4" "5").
Since this situation occurs quite often in practice, BSL+ supports one more
short-hand mechanism for list creation:
,@, also known as
unquote-splicing in keyword form. With this form, it is
straightforward to splice a nested list into a surrounding list. For example,
`(tr ,@(make-row '(3 4 5)))
translates into
(cons 'tr (make-row '(3 4 5)))
which is precisely what we need for our example.
Now consider the problem of creating an HTML table in our nested-list
representation. Here is a table of two rows with four cells each:
| '(table ((border "1")) |
| (tr (td "1") (td "2") (td "3") (td "4")) |
| (tr (td "2.8") (td "-1.1") (td "3.4") (td "1.3"))) |
The first nested lists tells HTML to draw a thin border around each cell in the
table; the other two nested lists represent a row each.
In practice, you want to create such tables with arbitrarily wide rows and
arbitrarily many rows. For now, we just deal with the first problem, which
requires a function that translates lists of numbers into HTML rows:
Instead of adding examples, we explore the behavior of these functions in
DrRacket’s interactions area:
| > (make-cell 2) |
(list 'td "2") |
| > (make-row '(1 2)) |
(list (list 'td "1") (list 'td "2")) |
These interactions show the creation of lists that represent a cell and a row.
To turn such row lists into actual rows of an HTML table representation, we need
to splice them into a list that starts with
'tr:
| ; List-of-numbers List-of-numbers -> ... nested list ... |
| ; creates an HTML table from two lists of numbers |
| (define (make-table row1 row2) |
| `(table ((border "1")) |
| (tr ,@(make-row row1)) |
| (tr ,@(make-row row2)))) |
This function consumes two lists of numbers and creates an HTML table
representation. With make-row, it translates the lists into lists of
cell representations. With ,@ these lists are spliced into the table
template:
| > (make-table '(1 2 3 4 5) '(3.5 2.8 -1.1 3.4 1.3)) |
(list 'table (list (list 'border "1")) '....) |
ThisThe dots are not part of the output.
application of make-table suggests another reason why people
write programs to create web pages rather than make them by hand.
Exercise 233. Develop alternatives to the following
expressions that use only
list and produce the same values:
Exercise 234. Create the function
make-ranking, which consumes
a list of ranked song titles and produces a list representation of an HTML
table. Consider this example:
| (define one-list |
| '("Asia: Heat of the Moment" |
| "U2: One" |
| "The White Stripes: Seven Nation Army")) |
If you apply
make-ranking to
one-list and display the
resulting web page in a browser, you see something like the screen
shot in
figure 85.
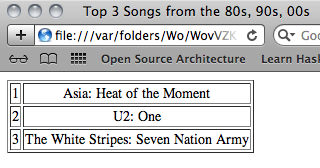
Figure 85: A web page generated with BSL+
Hint Although you could design a function that determines the rankings
from a list of strings, we wish you to focus on the creation of tables
instead. Thus we supply the following functions:
Before you use these functions, equip them with signatures and purpose
statements. Then explore their workings with interactions in DrRacket.
Accumulators expands the design recipe with a way to create
simpler functions for computing rankings than
ranking and
add-ranks.